
某商品经过连续两次降价,销售单价由原来 100 元降到 81 元。设平均每次降价的百分率为 x,根据题意可列方程为( )
A. 81(1-x)²=100 B. 100(1+x)²=81 C. 81(1+x)²=100 D. 100(1-x)²=81
D 【解析】试题解析:∵某种商品原价是100元,平均每次降价的百分率为x, ∴第一次降价后的价格为:100×(1?x), ∴第二次降价后的价格为:100×(1?x)×(1?x)= ∴可列方程为: 故选D. 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案科目:初中数学 来源:黑龙江省密山市2017-2018学年八年级上学期期中考试数学试卷 题型:填空题
等腰三角形一腰上的高与另一腰的夹角为50°,则这个等腰三角形顶角度数为______。
40°或140° 【解析】(1)当等腰三角形是锐角三角形时,如图①: ∵∠ACD=50°, ∴∠BAC=90°-∠ACD=40°; (2)当等腰三角形是钝角三角形时, 如图②: 当∠ACD=50°时,∠CAD=40°; ∴∠BAC=180°-∠CAD=140°. ∴这个等腰三角形顶角的度数为:40°或140°.查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题九年级人教版数学试卷(C卷) 题型:单选题
志愿者服务站为指导农民发展种植业进行技术培训,三期共培训95人,其中第一期培训20人,求每期培训人数的平均增长率,设平均增长率为x,根据题意列出的方程为( )
A. 20(1+x)2=95 B. 20(1+x)3=95
C. 20(1+x)+20(1+x)2=95 D. 20(1+x)+20(1+x)2=95﹣20
D 【解析】试题解析:设平均增长率为x,则第二期培训20(1+x)人,第三期培训 人, 根据题意得:20+20(1+x)+20(1+x)2=95. 故选D.查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题九年级人教版数学试卷(A卷) 题型:填空题
圆锥的侧面展开图的面积为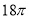 ,母线长为6,则圆锥的底面半径为________.
,母线长为6,则圆锥的底面半径为________.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题九年级人教版数学试卷(A卷) 题型:单选题
已知二次函数y=ax2+bx+c的图象如图,则下列判断正确是( )
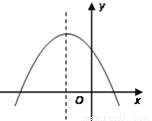
A. a<0,b>0,c>0 B. a<0,b<0,c<0 C. a<0,b<0,c>0 D. a>0,b<0,c>0
C 【解析】∵图象开口向下,∴a<0, ∵?<0,∴b<0, ∵图象交y轴的正半轴于一点,∴c>0. 故选:C.查看答案和解析>>
科目:初中数学 来源:河南省2017-2018学年八年级(上)第一次月考数学试卷 题型:解答题
如图1,四边形ABCD是正方形,G是CD边上的一个动点(点G与C、D不重合),以CG为一边在正方形ABCD外作正方形CEFG,连接BG,DE.我们探究下列图中线段BG、线段DE的长度关系及所在直线的位置关系.
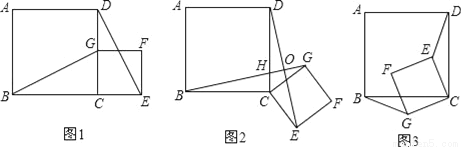
(1)猜想图1中线段BG、线段DE的长度关系及所在直线的位置关系;
(2)将图1中的正方形CEFG绕着点C按顺时针(或逆时针)方向旋转任意角度a,得到如图2、如图3情形.请你通过观察、测量等方法判断(1)中得到的结论是否仍然成立,并选取图2证明你的判断.
(1)BH⊥DE,即BG⊥DE,理由见解析. (2)BG=DE,BG⊥DE仍然成立,理由见解析. 【解析】试题分析:(1)根据正方形的性质,显然三角形BCG顺时针旋转90°即可得到三角形DCE,从而判断两条直线之间的关系; (2)结合正方形的性质,根据SAS仍然能够判定△BCG≌△DCE,从而证明结论. 【解析】 (1)BG=DE,BG⊥DE; ∵四边形ABCD和四...查看答案和解析>>
科目:初中数学 来源:河南省2017-2018学年八年级(上)第一次月考数学试卷 题型:解答题
如图,△ABC中,∠B=34°,∠ACB=104°,AD是BC边上的高,AE是∠BAC的平分线,求∠DAE的度数.
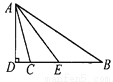
查看答案和解析>>
科目:初中数学 来源:广西南宁市2017年中考数学一模试卷 题型:解答题
如图,PA是⊙O的切线,A为切点,AC是⊙O的直径,AB是弦,PA∥BC交AB于点D.
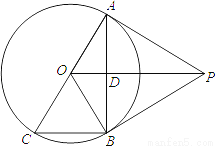
(1)求证:PB是⊙O的切线.
(2)当BC=2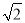 ,cos∠AOD=
,cos∠AOD=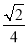 时,求PB的长.
时,求PB的长.
查看答案和解析>>
科目:初中数学 来源:广西岑溪市2018届九年级上学期期中抽考数学试卷 题型:单选题
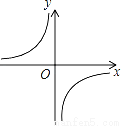
已知反比例函数y=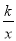 的图象如图所示,则二次函数y=2kx2﹣x+k2的图象大致为( )
的图象如图所示,则二次函数y=2kx2﹣x+k2的图象大致为( )
A. 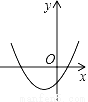 B.
B. 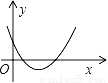 C.
C. 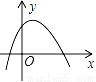 D.
D. 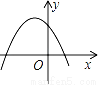
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com