
(﹣am)5•an=( )
A. ﹣a5+m B. a5+m C. a5m+n D. ﹣a5m+n
D 【解析】试题分析:(-am)5•an=-a5m+n. 故选D. 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:初中数学 来源:江苏省扬州市2016届九年级下学期二模数学试卷 题型:单选题
下列电视台的台标,是中心对称图形的是( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:2017年海南省中考数学模拟试卷 题型:单选题
如图,在△ABC中,∠CAB=65°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为( )
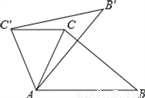
A. 35° B. 40° C. 50° D. 65°
C 【解析】试题解析:∵CC′∥AB, ∴∠ACC′=∠CAB=65°, ∵△ABC绕点A旋转得到△AB′C′, ∴AC=AC′, ∴∠CAC′=180°-2∠ACC′=180°-2×75°=30°, ∴∠CAC′=∠BAB′=30° 故选A.查看答案和解析>>
科目:初中数学 来源:2017年海南省中考数学模拟试卷 题型:填空题
如图,已知抛物线y=x2+bx+c经过点(0,﹣3),请你确定一个b的值,使该抛物线与x轴的一个交点在(1,0)和(3,0)之间.你确定的b的值是_____.
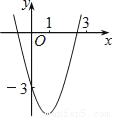
查看答案和解析>>
科目:初中数学 来源:2017年海南省中考数学模拟试卷 题型:单选题
如图,在平面直角坐标系中,点B,C,E在y轴上,Rt△ABC经过变换得到Rt△ODE.若点C的坐标为(0,1),AC=2,则这种变换可以是( )
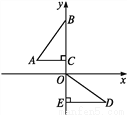
A. △ABC绕点C顺时针旋转90°,再向下平移3个单位长度
B. △ABC绕点C顺时针旋转90°,再向下平移1个单位长度
C. △ABC绕点C逆时针旋转90°,再向下平移1个单位长度
D. △ABC绕点C逆时针旋转90°,再向下平移3个单位长度
A 【解析】试题解析:根据图形可以看出,△ABC绕点C顺时针旋转90°,再向下平移3个单位可以得到△ODE. 故选A.查看答案和解析>>
科目:初中数学 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷(八) 题型:解答题
如图,抛物线y=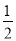 x2﹣
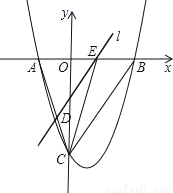
x2﹣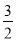 x﹣9与x轴交于A、B两点,与y轴交于点C,连接BC、AC.
x﹣9与x轴交于A、B两点,与y轴交于点C,连接BC、AC.
(1)求AB和OC的长;
(2)点E从点A出发,沿x轴向点B运动(点E与点A、B不重合),过点E作直线l平行BC,交AC于点D.设AE的长为m,△ADE的面积为s,求s关于m的函数关系式,并写出自变量m的取值范围;
(3)在(2)的条件下,连接CE,求△CDE面积的最大值;此时,求出以点E为圆心,与BC相切的圆的面积(结果保留π).
查看答案和解析>>
科目:初中数学 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷(八) 题型:解答题
先化简:(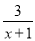 ﹣x+1)÷
﹣x+1)÷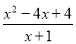 ,然后从﹣1≤x≤2中选一个合适的整数作为x的值代入求值.
,然后从﹣1≤x≤2中选一个合适的整数作为x的值代入求值.
查看答案和解析>>
科目:初中数学 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷(八) 题型:单选题
如图,小明从正面观察一个圆柱体邮筒和一个正方体箱子,看到的是( )
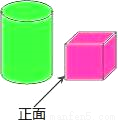
A.  B.
B.  C.
C. 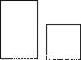 D.
D. 
查看答案和解析>>
科目:初中数学 来源:黄金30题系列 八年级数学 大题好拿分 题型:解答题
△ABC的三边满足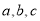 满足
满足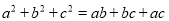 ,判断△ABC的形状并加以说明。
,判断△ABC的形状并加以说明。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com