练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    点到直线的距离是（ ）

    A. 点到直线上一点的连线 B. 点到直线的垂线

    C. 点到直线的垂线段 D. 点到直线的垂线段的长度

    D 【解析】试题解析：点到直线的距离是指点到直线的垂线段的长度，故选D．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：江苏省苏州市张家港市2016-2017学年九年级（上）期末数学试卷 题型：填空题

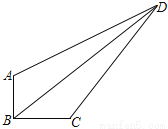
    （2016湖北省武汉市）如图，在四边形ABCD中，∠ABC＝90°，AB＝3，BC＝4，CD＝10，DA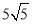＝，则BD的长为_______．

    ． 【解析】作DM⊥BC，交BC延长线于M，连接AC，如图所示： 则∠M=90°， ∴∠DCM+∠CDM=90°， ∵∠ABC=90°，AB=3，BC=4， ∴AC2=AB2+BC2=25， ∵CD=10，AD=5， ∴AC2+CD2=AD2， ∴△ACD是直角三角形，∠ACD=90°， ∴∠ACB+∠DCM=90°， ∴∠ACB=∠CD...

    查看答案和解析>>

    科目：初中数学 来源：北师大版数学七年级下册第一章整式乘法1.7整式的除法课时练习 题型：单选题

    15a3b÷（-5a2b）等于（ ）

    A. -3a B. -3ab C. a3b D. a2b

    A 【解析】15a3b÷（-5a2b）=[15÷(-5)]( a3÷a2)( b÷b) =-3a, 故选：A.

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年七年级数学人教版5.1相交线同步练习 题型：解答题

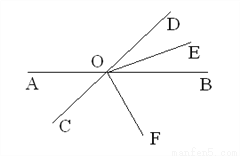
    .如图，直线AB，CD相交于点O ，OE平分∠BOD，OF平分∠COE，∠AOD：∠BOE=4:1，求∠AOF的度数。

    135° 【解析】本题需先根据∠AOD：∠BOE=4:1设∠AOD=4x°，∠BOE=x°，再根据角平分线的性质，分别求出各角的值，再利用角的和差即可求出结果． 【解析】 ∵∠AOD：∠BOE=4:1， ∴设∠AOD=4x°，则∠BOE=x°， ∵OE平分∠BOD， ∴∠BOD=2∠BOE=2x°， ∵∠AOD+∠BOD=180°， ∴6x=180， ...

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年七年级数学人教版5.1相交线同步练习 题型：单选题

    如图所示，按各组角的位置判断错误的是（ ）

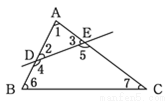
    A. ∠1和∠2是同旁内角 B. ∠3和∠4是内错角

    C. ∠5和∠6是同旁内角 D. ∠5和∠7是同旁内角

    C 【解析】根据同位角、内错角、同旁内角的定义进行解答即可． 【解析】 ∠1和∠2是同旁内角，故A选项正确； ∠3和∠4是内错角，故B选项正确； ∠5和∠6不是同旁内角，故C选项错误； ∠5和∠7是同旁内角，故D选项正确；， 故选：C.

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级下册 2.2 探索直线平行的条件（1） 同步练习 题型：填空题

    如图，已知直线a，b，c，d，e，且∠1=∠2，∠3=∠4，则a与c平行吗?为什么?

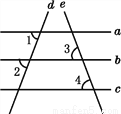
    【解析】
    a与c平行；

    理由：因为∠1=∠2 （_________________）

    所以a//b （__________________________________________）

    因为∠3=∠4 （_________________）

    所以b//c （__________________________________________）

    所以a//c （__________________________________________）

    已知 同位角相等，两直线平行 已知 同位角相等，两直线平行 平行于同一条直线的两条直线平行 【解析】因为∠1=∠2（已知） 所以a//b（同位角相等，两直线平行） 因为∠3=∠4（已知） 所以b//c（同位角相等，两直线平行） 所以a//c（平行于同一条直线的两条直线平行） 故答案为：已知；同位角相等，两直线平行；已知；同位角相等，两直线平行；平行于同一条直线的...

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级下册 2.2 探索直线平行的条件（1） 同步练习 题型：单选题

    下列说法正确的有(   )

    　 ①不相交的两条直线是平行线；②在同一平面内，两条直线的位置关系有两种；

    　 ③若线段AB与CD没有交点，则AB∥CD；④若a∥b，b∥c，则a与c不相交．

    A. 1个 B. 2个 C. 3个 D. 4个

    B 【解析】①错，在同一平面内时①才成立；②正确；③错，两线段平行是指它们所在直线没交点；④正确．故选B．

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下册 第二章 相交线与平行线 2.2 探索直线平行的条件 同位角及平行公理 同步课堂练习题 题型：填空题

    在同一平面内有四条直线a、b、c、d，已知：a∥d，b∥c，b∥d，则a和c的位置关系是_____.

    a∥c 【解析】∵a∥d，b∥c，b∥d∴a∥c故答案是a∥c.

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下2.2.1 用“同位角、第三直线”判定平行线 同步练习 题型：填空题

    如图,点B在DC上,BE平分∠ABD,∠ABE=∠C,试说明:BE∥AC.

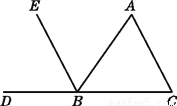
    解:因为BE平分∠ABD,

    所以∠ABE=∠DBE

    (_____________________). 

    因为∠ABE=∠C,

    所以∠DBE=∠C,

    所以BE∥AC(_____________________).

    角平分线的定义;同位角相等,两直线平行 【解析】根据角平分线的定义和平行线的判定填空，因为BE平分∠ABD, 所以∠ABE=∠DBE(角平分线的定义). 因为∠ABE=∠C, 所以∠DBE=∠C, 所以BE∥AC(同位角相等,两直线平行). 故答案为：角平分线的定义，同位角相等,两直线平行.

    查看答案和解析>>

    同步练习册答案