
科目:初中数学 来源:北京市通州区2017-2018学年第一学期期末初三数学统一检测试卷 题型:填空题
已知点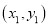 ,
, 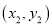 在反比例函数
在反比例函数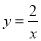 上,当
上,当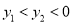 时,
时, 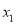 ,
, 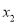 的大小关系是____________.
的大小关系是____________.
查看答案和解析>>
科目:初中数学 来源:山东省2017-2018学年七年级上学期期末考试数学试卷 题型:填空题
某商店把一种商品按标价的八折出售,获得的利润是进价的20%,该商品的标价为每件288元,则该商品的进价为每件_______元.
192 【解析】试题解析:设该商品的进价是x元,由题意得:(1+20%)x=288×0.8, 解得:x=192, 即该商品的进价为192元, 故答案为:192查看答案和解析>>
科目:初中数学 来源:山东省2017-2018学年七年级上学期期末考试数学试卷 题型:单选题
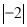 的相反数是( )
的相反数是( )
A. 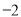 B.
B. 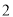 C.
C. 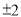 D.
D. 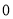
查看答案和解析>>
科目:初中数学 来源:北京市丰台区2018届九年级第一学期期末数学试卷 题型:解答题
在北京市开展的“首都少年先锋岗”活动中,某数学小组到人民英雄纪念碑站岗执勤,并在活动后实地测量了纪念碑的高度. 方法如下:如图,首先在测量点A处用高为1.5m的测角仪AC测得人民英雄纪念碑MN顶部M的仰角为35°,然后在测量点B处用同样的测角仪BD测得人民英雄纪念碑MN顶部M的仰角为45°,最后测量出A,B两点间的距离为15m,并且N,B,A三点在一条直线上,连接CD并延长交MN于点E. 请你利用他们的测量结果,计算人民英雄纪念碑MN的高度.
(参考数据:sin35°≈0.6,cos35°≈0.8,tan35°≈0.7)

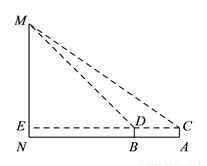
查看答案和解析>>
科目:初中数学 来源:北京市丰台区2018届九年级第一学期期末数学试卷 题型:填空题
如图,等边三角形ABC的外接圆⊙O的半径OA的长为2,则其内切圆半径的长为__________.
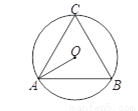
查看答案和解析>>
科目:初中数学 来源:北京市丰台区2018届九年级第一学期期末数学试卷 题型:单选题
如图,点A为函数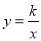 (x>0)图象上的一点,过点A作x轴的平行线交y轴于点B,连接OA,如果△AOB的面积为2,那么k的值为( )
(x>0)图象上的一点,过点A作x轴的平行线交y轴于点B,连接OA,如果△AOB的面积为2,那么k的值为( )
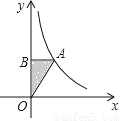
A. 1 B. 2 C. 3 D. 4
D 【解析】设点A坐标为(m,n),则有AB=m,OB=n,由题意可得: =2,所以mn=4, 又点A在双曲线上,所以k=mn=4, 故选D.查看答案和解析>>
科目:初中数学 来源:2017-2018学年七年级数学下册(人教版):期中检测题 题型:填空题
若A(a,-b)是第二象限内的一点,则点B(a2,b-1)在第__________象限.
四. 【解析】根据第二象限内点的横坐标是负数,纵坐标是正数求出a、b的取值范围,然后判断出点B的横坐标与纵坐标的正负情况,再根据各象限内点的坐标特征解答. 【解析】 ∵A(a,-b)是第二象限的一点, ∴a<0,-b>0, ∴a2>0,b-1<0, ∴点B(a2,b-1)在第四象限. 故答案为:四.查看答案和解析>>
科目:初中数学 来源:福建省泉州市2016-2017学年七年级下学期期末考试数学试卷 题型:解答题
我们知道:经过对称中心的直线可以把一个中心对称图形的面积平分.
请运用这一性质解决下列问题:(注意:以下作图工具仅限于一把无刻度的直尺,要体现作图过程且保留作图痕迹)

(1)如甲图,画一条直线把矩形分成面积相等的两部分;
(2)如乙图,画一条直线把乙图分成面积相等的两部分(画出3种不同的分割线).
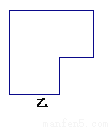


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com