练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，在矩形ABCD中，E为AD边上的一点，过C点作CF⊥CE交AB的延长线于点F.

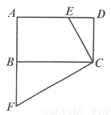
    （1）求证：△CDE∽△CBF；

    （2）若B为AF的中点，CB=3，DE=1，求CD的长.

    （1）证明见解析；（2）CD= 【解析】试题分析：（1）如图，通过证明∠D=∠1，∠2=∠4即可得； （2）由△CDE∽△CBF，可得CD：CB=DE：BF，根据B为AF中点，可得CD=BF，再根据CB=3，DE=1即可求得. 试题解析：（1）∵四边形ABCD是矩形， ∴∠D=∠1=∠2+∠3=90° ， ∵CF⊥CE， ∴∠4+∠3=90°， ∴∠2=∠...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：重庆市江津区2017-2018学年八年级上学期第二次六校联考数学试卷 题型：填空题

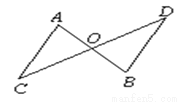
    如图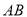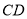， 、相交于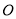，且OA=OB，观察图形：图中隐含一个相等的角，联想“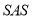”，只需补充条件 ，则有≌.

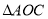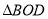    OC=OD 【解析】试题解析：OC=OD，. 理由是：∵在△AOC和△BOD中. . ∴△AOC≌△BOD（SAS），. 故答案为：OC=OD．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年第一学期期末复习备考之精准复习模拟题九年级北师大版数学试卷（C卷） 题型：解答题

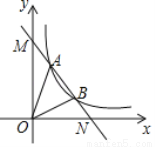
    如图，一次函数y=kx+b与反比例函数y=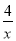（x＞0）的图象交于A（m，4），B（2，n）两点，与坐标轴分别交于M、N两点．

    （1）求一次函数的解析式；

    （2）根据图象直接写出不等式kx+b﹣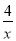＞0的解集；

    （3）求△AOB的面积；

    （4）若点P在x轴上、点Q在y轴上，且以P、Q、A、B为顶点的四边形是平行四边形，请直接写出点P、Q的坐标．

    （1）一次函数的解析式为y=﹣2x+6；（2）x的取值范围为1＜x＜2；（3）S△AOB= 3；（4）（1，0），（0，2）或（-1，0），（0，-2）． 【解析】试题分析：（1）先根据反比例函数解析式求出点A、点B的坐标，然后利用待定系数法即可求出一次函数的解析式； （2）根据函数图象即可得； （3）先求出直线AB与坐标轴的交点M、N的坐标，然后用△MON的面积减△AOM的面积...

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年第一学期期末复习备考之精准复习模拟题九年级北师大版数学试卷（C卷） 题型：单选题

    关于x的一元二次方程(a－1)x2＋x＋a2＋3a－4＝0有一个实数根是x＝0．则a的值为（ ）．

    A. 1或－4 B. 1 C. －4 D. －1或4

    C 【解析】本题根据一元二次方程的根的定义、一元二次方程的定义可得：

    查看答案和解析>>

    科目：初中数学 来源：北京四中2018届上学期初中九年级期中考试数学试卷 题型：解答题

    青青书店购进了一批进价为每本20元的中华传统文化丛书. 在销售的过程中发现，这种图书每天的销售数量y（本）与销售单价x（元）满足一次函数关系：y=-3x+108（20<x<36）. 如果销售这种图书每天的利润为p（元），那么销售单价定为多少元时，每天获得的利润最大?最大利润是多少?

    销售单价定为28元时，每天获得的利润最大，最大利润是192元. 【解析】试题分析：由利润=每本书的利润×数量就可以得出解析式，再根据函数的性质即可得到最大利润. 试题解析：p=（x-20）（-3x+108）=-3x2+168x-2160=-3（x-28）2+192， ∵20

    查看答案和解析>>

    科目：初中数学 来源：北京四中2018届上学期初中九年级期中考试数学试卷 题型：填空题

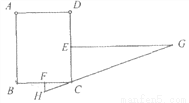
    “今有邑，东西七里，南北九里，各开中门，出东门一十五里有木，问：出南门几何步而见木?”这段话摘自《九章算术》，意思是说：如图，矩形城池ABCD，城墙CD长9里，城墙BC长7里，东门所在的点E，南门所在的点F分别是CD，BC的中点，EG⊥CD，EG=15里，FH⊥BC，点C在HG上，问FH等于多少里?答案是FH=________里.

    1.05 【解析】∵EG⊥CD，FH⊥BC，HG经过C点， ∴FC∥EG，EC∥FH， ∴∠HFC=∠CEG=90°，∠FHC=∠ECG， ∴△GEC∽△CFH， ∴ , ∵CD=9里，BC=7里，EG=15里， ∴FC=3.5里，EC=4.5里， ∴ ， 解得：FH=1.05里， 故答案为：1.05．

    查看答案和解析>>

    科目：初中数学 来源：北京四中2018届上学期初中九年级期中考试数学试卷 题型：单选题

    若A（1，y1），B（2，y2）两点都在反比例函数y=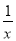的图象上，则y1与y2的大小关系是（ ）.

    A. y1< y2 B. y1= y2 C. y1> y2 D. 无法确定

    C 【解析】∵A（1，y1），B（2，y2）两点都在反比例函数y=的图象上， ∴1? y1=1,2? y2=1， 解得：y1=1, y2=， ∵1>， ∴y1>y2. 故选C.

    查看答案和解析>>

    科目：初中数学 来源：2017年甘肃省张掖市中考数学三模试卷 题型：填空题

    计算： =　 　．

    a. 【解析】试题解析：原式 故答案为：

    查看答案和解析>>

    科目：初中数学 来源：2017年湖北省随州市中考数学模拟试卷 题型：解答题

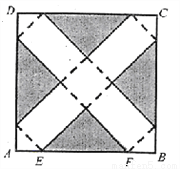
    如图，在边长为24cm的正方形纸片ABCD上，剪去图中阴影部分的四个全等的等腰直角三角形，再沿图中的虚线折起，折成一个长方体形状的包装盒(A、B、C、D四个顶点正好重合于底面上一点)．已知E、F在AB边上，是被剪去一个等腰直角三角形斜边的两个端点，设AE＝BF＝xcm．

    (1)若折成的包装盒恰好是正方体，试求这个包装盒的体积V；

    (2)某广告商要求包装盒的表面(不含下底面)面积S最大，试问x应取何值？

    （1）432 ；（2）384. 【解析】试题分析：（1）根据已知得出这个正方体的底面边长NQ=ME=x，EF=ME=2x，再利用AB=24cm，求出x即可得出这个包装盒的体积V； （2）利用已知表示出包装盒的表面，进而利用函数最值求出即可． 【解析】 （1）根据题意，设AE=BF=x（cm），折成的包装盒恰好是个正方体， 知这个正方体的底面边长NQ=ME=x，则QE=QF...

    查看答案和解析>>

    同步练习册答案