
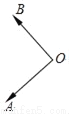
如图,向量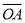 与
与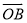 均为单位向量,且OA⊥OB,令
均为单位向量,且OA⊥OB,令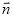 =
=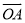 +
+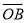 ,则
,则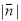 =( )
=( )
A. 1 B. 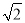 C.
C. 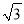 D. 2
D. 2
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案科目:初中数学 来源:北京市分校2017-2018学年度第一学期期中初二数学试卷 题型:解答题
在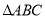 中,
中,
(1)如图1, 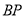 为
为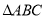 的角平分线,
的角平分线, 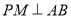 于
于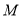 ,
, 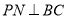 于
于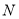 ,
, 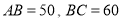 ,请直接写出
,请直接写出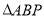 与
与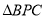 面积的比值;
面积的比值;
(2)如图2,分别以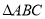 的边
的边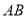 、
、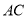 为边向外作等边三角形
为边向外作等边三角形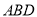 和
和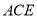 ,
, 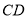 与
与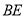 相交于点
相交于点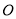 ,求证:BE=CD;
,求证:BE=CD;
(3)在(2)的条件下判断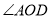 与
与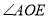 的数量关系,并加以证明.
的数量关系,并加以证明.
(注:可以直接应用等边三角形三边相等,每个角为60°)
查看答案和解析>>
科目:初中数学 来源:福建省2016-2017学年八年级下学期期末考试数学试卷 题型:单选题
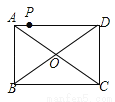
如图,点P是矩形ABCD的边AD上的一动点,矩形的两条边AB、BC的长分别是6和8,则点P到矩形的两条对角线AC和BD的距离之和是( )
A.4.8 B.5 C.6 D.7.2
A. 【解析】 试题分析:连接OP,∵矩形的两条边AB、BC的长分别为6和8,∴S矩形ABCD=AB•BC=48,OA=OC,OB=OD,AC=BD=10,∴OA=OD=5,∴S△ACD=S矩形ABCD=24,∴S△AOD=S△ACD=12,∵S△AOD=S△AOP+S△DOP=OA•PE+OD•PF =×5×PE+×5×PF=(PE+PF)=12,解得:PE+PF=4.8.故选...查看答案和解析>>
科目:初中数学 来源:上海市黄浦区2018届九年级上学期期末调研测试数学试卷(WORD版) 题型:填空题
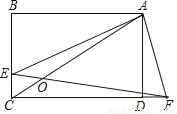
如图,点E为矩形ABCD边BC上一点,点F在边CD的延长线上,EF与AC交于点O,若CE:EB=1:2,BC:AB=3:4,AE⊥AF,则CO:OA=_____.
查看答案和解析>>
科目:初中数学 来源:上海市黄浦区2018届九年级上学期期末调研测试数学试卷(WORD版) 题型:填空题
已知△ABC ∽△DEF,其中顶点A、B、C分别对应顶点D、E、F,如果∠A=40°,∠E=60°,那么∠C=_______度.
80 【解析】因为△ABC ∽△DEF,所以∠A=∠D, ∠B=∠E, ∠C=∠F,因为∠A=40°,∠E=60°, 所以∠B=60°,所以∠C=180°―40°―60°=80°,故答案为: 80.查看答案和解析>>
科目:初中数学 来源:北京市西城外国语学校2017-2018学年度第一学期八年级数学期中试卷 题型:解答题
阅读下列材料:
利用完全平方公式,可以将多项式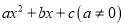 变形为
变形为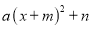 的形式, 我们把这样的变形方法叫做多项式
的形式, 我们把这样的变形方法叫做多项式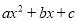 的配方法.运用多项式的配方法及平方差公式能对一些多项式进行分解因式.例如:
的配方法.运用多项式的配方法及平方差公式能对一些多项式进行分解因式.例如: 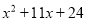 =
=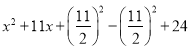
=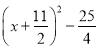
= =
=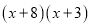
根据以上材料,解答下列问题:
(1)用多项式的配方法将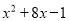 化成
化成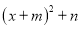 的形式;
的形式;
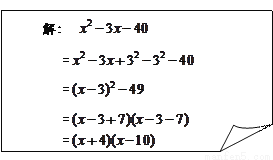
(2)下面是某位同学用配方法及平方差公式把多项式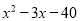 进行分解因式的解答过程:
进行分解因式的解答过程:
老师说,这位同学的解答过程中有错误,请你找出该同学解答中开始出现错误的地方,并用“ ”标画出来,然后写出完整的、正确的解答过程:
(3)求证:x,y取任何实数时,多项式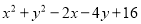 的值总为正数.
的值总为正数.
查看答案和解析>>
科目:初中数学 来源:北京市西城外国语学校2017-2018学年度第一学期八年级数学期中试卷 题型:解答题
解分式方程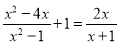
查看答案和解析>>
科目:初中数学 来源:北京市西城外国语学校2017-2018学年度第一学期八年级数学期中试卷 题型:单选题
如图,B,D,E,C四点共线,且△ABD≌△ACE,若∠AEC=105°,则∠DAE的度数等于( ).

A. 30° B. 40° C. 50° D. 65°
A 【解析】【解析】 ∵△ABD≌△ACE,∴∠ADB=∠AEC=105°,∴∠ADE=∠AED=75°,∴∠DAE=180°﹣75°﹣75°=30°,故选A.查看答案和解析>>
科目:初中数学 来源:浙江省余姚市2017-2018学年八年级上学期期中考试数学试卷 题型:解答题
已知:如图,直线AD与BC交于点O,OA=OD,OB=OC.求证:AB∥CD.
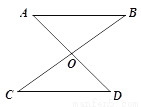
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com