
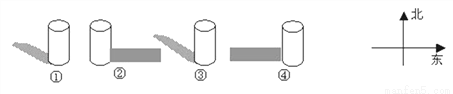
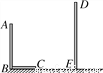
下图是小红在某天四个时刻看到一根木棒及其影子的情况,那么她看到的先后顺序是________ .
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:初中数学 来源:浙江杭州上城区建兰中学2018届九年级上学期期中数试卷 题型:单选题
已知一个扇形的半径为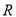 、圆心角为
、圆心角为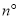 ,当这个扇形的面积与一个直径为
,当这个扇形的面积与一个直径为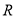 的圆面积相等时,则这个扇形的圆心角
的圆面积相等时,则这个扇形的圆心角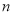 的度数是( )
的度数是( )
A. 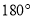 B.
B. 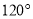 C.
C. 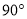 D.
D. 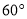
查看答案和解析>>
科目:初中数学 来源:人教版九年级下册数学全册综合测试一 题型:解答题
海船以5海里/小时的速度向正东方向行驶,在A处看见灯塔B在海船的北偏东60°方向,2小时后船行驶到C处,发现此时灯塔B在海船的北偏西45°方向,求此时灯塔B到C处的距离。

查看答案和解析>>
科目:初中数学 来源:人教版九年级下册数学全册综合测试一 题型:单选题
若一个三角形三边之比为3:5:7,与它相似的三角形的最长边的长为21,则最短边的长为
A. 15 B. 10 C. 9 D. 3
C 【解析】 试题分析:设最短边的长为x,根据相似三角形的性质即可列方程求解. 设最短边的长为x,由题意得 解得 故选C.查看答案和解析>>
科目:初中数学 来源:人教版九年级下册数学 第29章 投影与视图 单元检测卷 题型:解答题
有一个几何体的形状为直三棱柱,右图是它的主视图和左视图.
(1)请补画出它的俯视图,并标出相关数据;
(2)根据图中所标的尺寸(单位:厘米),计算这个几何体的全面积.
(1)答案见解析;(2)全面积是120平方厘米. 【解析】分析:(1)观察图形可知,俯视图是一个长8宽3的长方形,据此画出图形即可; (2)先根据勾股定理得到斜边长为10厘米,再根据表面积=3个长方形的面积+2个三角形的面积,列出算式计算即可求解. 本题解析: 【解析】 (1)如图所示; (2)由勾股定理得斜边长为10厘米,S底=×8×6=24(平方厘米),S侧=(...查看答案和解析>>
科目:初中数学 来源:人教版九年级下册数学 第29章 投影与视图 单元检测卷 题型:填空题
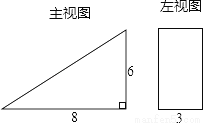
三棱柱的三视图如图所示,△EFG中,EF=10cm,EG=16cm,∠EGF=30°,则AB的长为________cm .
查看答案和解析>>
科目:初中数学 来源:人教版九年级下册数学 第29章 投影与视图 单元检测卷 题型:单选题
把下列图标折成一个正方体的盒子,折好后与“中”相对的字是( )

A. 祝 B. 你 C. 顺 D. 利
C 【解析】【解析】 这是一个正方体的平面展开图,共有六个面,其中面“考”与面“顺”相对,面“你”与面“试”相对,面“祝”与面“利”相对.故选C.查看答案和解析>>
科目:初中数学 来源:2017-2018学年八年级数学人教版上册 第13章 轴对称 单元测试卷 题型:单选题
已知等腰三角形的一边长为6,一个内角为60°,则它的周长是( )
A. 12 B. 15 C. 18 D. 20
C 【解析】试题解析:∵等腰三角形的一个内角为60°, ∴此等腰三角形是等边三角形. ∵一边长为6, ∴它的周长为18. 故选C.查看答案和解析>>
科目:初中数学 来源:2017-2018学年九年级数学北师大版上册 第5章 投影与视图 单元测试卷 题型:填空题
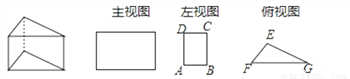
如图,AB和DE是直立在地面上的两根立柱,AB=7米,某一时刻AB在阳光下的投影BC=4米,在测量AB的投影时,同时测量出DE在阳光下的投影长为6米,则DE的长为________米.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com