
某商店9月份的利润是2500元,要使11月的利润达到3600元,平均每月增长的百分率是多少?
20% 【解析】 如果设平均每月增长的百分率是x,那么10月份的利润是2500(1+x)元,11月份的利润是2500(1+x)2元,而此时利润是3600元,根据11月份的利润不变,列出方程。 设平均每月增长的百分率是x, 依题意,得2500(1+x)2=3600, 解得x1=0.2,x2=-2.2(不合题意,舍去). 所以平均每月增长的百分率应该是20%。 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:江苏省东部分校2017-2018学年八年级上学期期末考试数学试卷 题型:填空题
将直线y=-3x-2向上平移3个单位长度后得到的直线解析式是___________.
y=-3x+1 【解析】试题解析:由“上加下减”的原则可知,把直线y=-3x-2向上平移3个单位长度后所得直线的解析式为:y=-3x-2+3,即y=-3x+1. 故答案为:y=-3x+1.查看答案和解析>>
科目:初中数学 来源:江西省萍乡市2017-2018学年七年级上学期期末考试数学试卷 题型:解答题
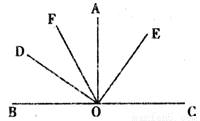
如图,∠AOB=∠AOC=90 ,∠DOE=90
,∠DOE=90 ,OF平分∠AOD,∠AOE= 36
,OF平分∠AOD,∠AOE= 36 .
.
(1)求∠COD的度数;(2)求∠BOF的度数.
查看答案和解析>>
科目:初中数学 来源:江西省萍乡市2017-2018学年七年级上学期期末考试数学试卷 题型:单选题
某中学为检查七年级学生的视力情况,对七年级全体300名学生进行了体检,并制作了如图所示的扇形统计图,由该图可以看出七年级学生视力不良的学生有( )

A. 45人 B. 120人 C. 135人 D. 165人
D 【解析】试题解析:由题意可得: 视力不良所占的比例为:40%+15%=55%, 视力不良的学生数:300×55%=165(人). 故选D.查看答案和解析>>
科目:初中数学 来源:江苏省泰兴市2018届九年级上学期期末考试数学试卷 题型:解答题
在△ABC中,AB=AC,BC=12,E为边AC的中点,
(1)如图1,过点E作EH⊥BC,垂足为点H,求线段CH的长;
(2)作线段BE的垂直平分线分别交边BC、BE、AB于点D、O、F.
①如图2,当∠BAC=90°时,求BD的长;
②如图3,设tan∠ACB=x,BD=y,求y与x之间的函数表达式和tan∠ACB的最大值.

查看答案和解析>>
科目:初中数学 来源:江苏省泰兴市2018届九年级上学期期末考试数学试卷 题型:填空题
如图,在平面直角坐标系中,抛物线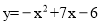 与直线
与直线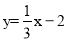 相交于点B、C,点P为直线BC上方的抛物线上的一动点, PQ⊥x轴交BC于点Q,PG⊥BC于点G,点M为线段PQ的中点,则线段GM的最大值为_________.
相交于点B、C,点P为直线BC上方的抛物线上的一动点, PQ⊥x轴交BC于点Q,PG⊥BC于点G,点M为线段PQ的中点,则线段GM的最大值为_________.
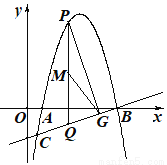
查看答案和解析>>
科目:初中数学 来源:江苏省泰兴市2018届九年级上学期期末考试数学试卷 题型:填空题
在泰州市举行的大阅读活动中,小明同学发现自己的一本书的宽与长之比为黄金比.已知这本书的长为20 cm,则它的宽为________cm.(结果保留根号)
() 【解析】设它的宽为xcm.由题意得 . ∴ .查看答案和解析>>
科目:初中数学 来源:甘肃省天水市2017-2018学年七年级上学期期末模四考试数学试卷 题型:解答题
已知平面上四点A、B、C、D,如图:
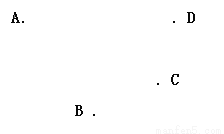
(1)画直线AB;(2)画射线AD;
(3)直线AB、CD相交于点E;(4)连结AC、BD相交于点F;
答案见解析. 【解析】试题分析:根据直线、射线、线段的定义按语句进行画图即可得. 试题解析:如图所示.查看答案和解析>>
科目:初中数学 来源:江苏省扬州市邗江区2018届九年级上学期期末考试数学试卷 题型:单选题
⊙O的半径为10,两平行弦AC,BD的长分别为12,16,则两弦间的距离是( )
A. 2 B. 14 C. 6或8 D. 2 或14
D 【解析】试题解析:如图① 作OE⊥AC垂足为E,交BD于点F, ∵OE⊥AC,ACBD, ∴OF⊥BD, 在Rt△AOE中 同理可得: OF=6cm, ∴EF=OE?OF=8?6=2cm; 如图② 同理可得:EF=OE+OF=8+6=14cm 综上所述两弦之间的距离为2cm或14cm. 故选D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com