
�ڡ�ABC�У�AB��10��AC��2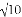 ��BC���ϵĸ�AD��6������һ��BC����_______��
��BC���ϵĸ�AD��6������һ��BC����_______��
���𰸡�10��6
������������������������⻭��ͼ�Σ���ͼ��ʾ��
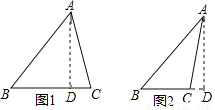
��ͼ1��ʾ��AB=10��AC=2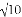 ��AD=6��
��AD=6��
��Rt��ABD��Rt��ACD��
���ݹ��ɶ����ã�BD=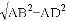 =8��CD=
=8��CD=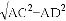 =2��
=2��
��ʱBC=BD+CD=8+2=10��
��ͼ2��ʾ��AB=10��AC=2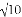 ��AD=6��
��AD=6��
��Rt��ABD��Rt��ACD��
���ݹ��ɶ����ã�BD=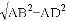 =8��CD=
=8��CD=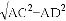 =2��
=2��
��ʱBC=BD-CD=8-2=6��
��BC�ij�Ϊ6��10��
�����͡������
��������
12
��ƽ��ֱ������ϵ�У���֪һ�κ���y=2x+1��ͼ��P1��x1��y1����P2��x2��y2�����㣬��x1��x2����y1 ______ y2�����������������=����
�� �������������������һ�κ���y=2x+1��k=2��0�� ��y��x����������� ��x1��x2�� ��y1��y2��
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ʡ������2017-2018ѧ����꼶12���¿���ѧ�Ծ� ���ͣ������
��ֱ֪��y=3x��y=��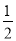 x��4��
x��4��
��1��������ֱ�ߵĽ������ꣻ
��2��������ֱ����x��Χ�ɵ�ͼ�ε������
��1������ ������2��. �������������������1��������ֱ���ཻ�����⣬�ⷽ���� ���ɵõ���ֱ�ߵĽ������ꣻ ��2���������ֱ������Ľ������꣬Ȼ����������������ʽ��⣮ ���������(1)������������������ã� ������ֱ�ߵĽ������꣨�� ���� (2) �� �� ����Ľ�������Ϊ ����ԭ��ľ���Ϊ��ֱ������Χ�������ε�һ�߳��ȣ� ��(1)��֪��ֱ�ߵĽ���Ϊ���� ����...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ2018����꼶12���¿���ѧ�Ծ� ���ͣ������
��֪һ�����ݣ�3��5��x��7��9��ƽ����Ϊ6����x=______��
6. ���������������� ������֪����3+5+x+7+9����5=6����ã�x=6���ʴ�Ϊ��6���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���˽̰���꼶�ϲ���ѧ 21.3ʵ��������һԪ���η��̣�1�� ���� ���ͣ���ѡ��
Ϊִ�С�����һ�������ߣ�ij����2012��Ͷ���������2500��Ԫ��Ԥ��2014��Ͷ��3600��Ԫ����������Ͷ��������ѵ���ƽ�������ٷ���Ϊx�������з�����ȷ���ǣ� ��
A. 2500x2=3600 B. 2500(1+x)2=3600
C. 2500(1+x%)2=3600 D. 2500(1+x)+2500(1+x)2=3600
B �����������������2014��Ͷ��Ϊ2500��1+x����2015��Ͷ��Ϊ2500��1+x����1+x������2500��1+x��2=3600�� ��ѡB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��֣�ݶ���ѧ��2017-2018ѧ����ѧ������ѧҵˮƽ���� ���꼶��ѧ�Ծ� ���ͣ������
��֪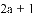
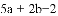
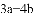
���𰸡�
�����������������������֪�ó�2a+1=9��5a+2b-2=16�����a b������������ɣ�
�������
��������ã�2a+1=32=9��5a+2b-2=16��
��a=4��b=-1��
��3a-4b=16��
��3a-4b��ƽ�����ǡ�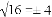 .
.
�����͡������
��������
17
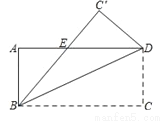
��ͼ����������ABCD�ضԽ���BD�۵���ʹ��C����C�䴦��BC�佻AD�ڵ�E��
��1�����жϡ�BDE����״����˵�����ɣ�
��2����AB=4��AD=8�����BDE�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��֣�ݶ���ѧ��2017-2018ѧ����ѧ������ѧҵˮƽ���� ���꼶��ѧ�Ծ� ���ͣ���ѡ��
������y=��m��1��x|m|��5��һ�κ�������m��ֵΪ��������
A. ��1 B. ��1 C. 1 D. 2
���𰸡�B
����������������ã�|m|=1��m?1��0��
���m=��1��m��1��
���ԣ�m=?1.
��ѡB.
�����͡���ѡ��
��������
7
��ͼ�Ǽס���������ijʱ���ٶ���ʱ��仯��ͼ�����н��۴�����ǣ�������
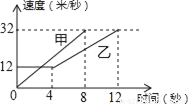
A. ��ǰ4����ʻ��·��Ϊ48��
B. ��0��8���ڼ��ٶ�ÿ������4��/��
C. ��������3��ʱ��ʻ��·�����
D. ��4��8���ڼ��ٶȶ������ҵ��ٶ�
C �����������������A������ͼ��ɵã���ǰ4����ʻ��·��Ϊ12��4=48�ף���ȷ�� B������ͼ��ã���0��8���ڼ��ٶ�ÿ������4����/����ȷ�� C������ͼ��ɵ���������3��ʱ��ʻ��·�̲���ȣ��ʱ�ѡ����� D����4��8���ڼ��ٶȶ������ҵ��ٶȣ���ȷ�� ��ѡC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���˽̰���꼶��ѧ�ϲᾭ���Ծ� ��21�� һԪ���η���Τ�ﶨ�� ���Ծ� ���ͣ������
��֪����x��һԪ���η���x2����2k��1��x��k2��2k��0������ʵ����x1��x2��
��1����ʵ��k��ȡֵ��Χ��
��2���Ƿ����ʵ��k��ʹ��x1��x2��x12��x22��0�����������ڣ������k��ֵ���������ڣ���˵�����ɣ�
(1)��k��ʱ��ԭ����������ʵ����(2)������ʵ��k��ʹ��x1��x2��x12��x22��0���� �������������������1������һԪ���η��̸����б�ʽ�г�����ʽ����֮���ɣ���2����������Τ�ﶨ�����. ��������� ��1�� ����� ��2���� �� �ɸ���ϵ���Ĺ�ϵ�ɵã� ����ã� �� ����ã� �� ��. ���ڵ�ȡֵ��ΧΪ�� �ʲ�����kʹ�� ...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���˽̰���꼶��ѧ�ϲᾭ���Ծ� ��21�� һԪ���η���Τ�ﶨ�� ���Ծ� ���ͣ���ѡ��
����������һԪ���η���x2+2x��6=0����������ȵĸ������2��2�µ�ֵ�ǣ� ��
A. 10 B. 16 C. ��2 D. ��10
A �������� �� �� . �� . �� -�ڵ� . ��ѡA.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������� 2017-2018ѧ�� ���꼶��ѧ�ϲ� һԪ���η��� ��ʽ�ֽⷨ ר����ϰ�����𰸣� ���ͣ������
��֪(a+b)2-2(a+b)-3=0����a+b=_______________.
3��1 ����������a+b����һ������,ʮ�����, (a+b)2-2(a+b)-3=0, (a+b-3)(a+b+1)=0, a+b-3=0,a+b+1=0, ����a+b=3,a+b=-1.�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com