
科目: 来源:江西省2018届九年级上学期第四次月考数学试卷 题型:解答题
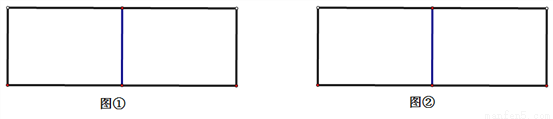
如图是由两个全等的矩形拼在一起的图形,请仅用无刻度的直尺,直接在图中用连线的方式按要求画出图形,并用字母表示所画图形.
(1)在图①中画出一个平行四边形(要求不与原矩形重合);
(2)在图②中画出一个菱形.
查看答案和解析>>
科目: 来源:江西省2018届九年级上学期第四次月考数学试卷 题型:解答题
抚州市某楼盘准备以每平方米8000元的均价对外销售,由于国务院有关房地产的新政策出台后,购房者持币观望,房地产开发商为了加快资金周转,对价格经过两次下调后,决定以每平方米6480元的均价开盘销售.
(1)求平均每次下调的百分率.
(2)某人准备以开盘价均价购买一套100平方米的住房,开发商给予以下两种优惠方案以供选择:①打9.8折销售;②不打折,一次性送装修费每平方米80元,请通过计算说明哪种方案更优惠?
查看答案和解析>>
科目: 来源:江西省2018届九年级上学期第四次月考数学试卷 题型:解答题
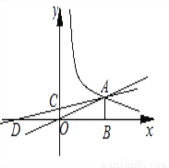
如图,O是坐标原点,直线OA与双曲线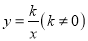 在第一象限内交于点A,过点A作AB⊥x轴,垂足为B,若OB=4,tan∠AOB=
在第一象限内交于点A,过点A作AB⊥x轴,垂足为B,若OB=4,tan∠AOB=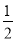 .
.
(1)求双曲线的解析式;
(2)直线AC与y轴交于点C(0,1),与x轴交于点D,求D点的坐标.
查看答案和解析>>
科目: 来源:江西省2018届九年级上学期第四次月考数学试卷 题型:解答题
有三张正面分别标有数字:-1,1,2的卡片,它们除数字不同外其余全部相同,现将它们背面朝上,洗匀后从中随机抽出一张记下数字,放回洗匀后再从中随机抽出一张记下数字.
(1)请用列表或画树形图的方法(只选其中一种),表示两次抽出卡片上的数字的所有结果;
(2)将第一次抽出的数字作为点的横坐标x,第二次抽出的数字作为点的纵坐标y,求点(x,y)落在双曲线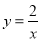 上的概率.
上的概率.
查看答案和解析>>
科目: 来源:江西省2018届九年级上学期第四次月考数学试卷 题型:解答题
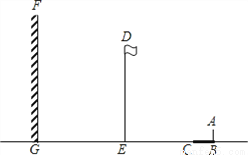
如图,阳光下,小亮的身高如图中线段AB所示,他在地面上的影子如图中线段BC所示,线段DE表示旗杆的高,线段FG表示一堵高墙.
(1)请你在图中画出旗杆在同一时刻阳光照射下形成的影子,并用线段表示;
(2)如果小亮的身高AB=1.6m,他的影子BC=2.4m,旗杆的高DE=15m,旗杆与高墙的距离EG=16m,请求出旗杆的影子落在墙上的长度.
查看答案和解析>>
科目: 来源:江西省2018届九年级上学期第四次月考数学试卷 题型:解答题
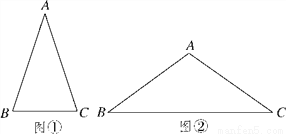
我们定义:等腰三角形中底边与腰的比叫作底角的邻对(can).如图①,在△ABC中,AB=AC,底角∠B的邻对记作canB,这时canB=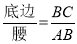 .容易知道一个角的大小与这个角的邻对值是一一对应的,根据上述角的邻对的定义,解下列问题:
.容易知道一个角的大小与这个角的邻对值是一一对应的,根据上述角的邻对的定义,解下列问题:
(1) . can30°=______ __;
(2) . 如图②,已知在△ABC中,AB=AC,canB=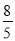 ,S△ABC=24,求△ABC的周长.
,S△ABC=24,求△ABC的周长.
查看答案和解析>>
科目: 来源:江西省2018届九年级上学期第四次月考数学试卷 题型:解答题
如图①是一个新款水杯,水杯不盛水时按如图②所示的位置放置,这样可以快速晾干杯底,干净透气;将图②的主体部分抽象成图③,此时杯口与水平直线的夹角为37°,四边形ABCD可以看作矩形,测得AB=10cm,BC=8cm,过点A作AF⊥CE,交CE于点F.
(1)求∠BAF的度数;
(2)求点A到水平直线CE的距离AF的长 (参考数据sin37°≈0.6,cos37°≈0.8,tan37°≈0.75).

查看答案和解析>>
科目: 来源:江西省2018届九年级上学期第四次月考数学试卷 题型:解答题
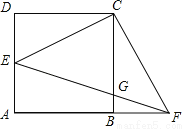
如图,四边形ABCD是边长为1的正方形,点E在AD边上运动,且不与点A和点D重合,连结CE,过点C作CF⊥CE交AB的延长线于点F,EF交BC于点G.
(1)求证:△CDE≌△CBF;
(2)当DE=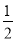 时,求CG的长;
时,求CG的长;
(3)连结AG,在点E运动过程中,四边形CEAG能否为平行四边形?若能,求出此时DE的长;若不能,说明理由.
查看答案和解析>>
科目: 来源:江西省2018届九年级上学期第四次月考数学试卷 题型:解答题
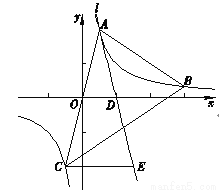
如图,在平面直角坐标系xOy中,点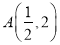 ,
, 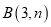 在反比例函数
在反比例函数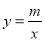 (m为常数)的图象上,连接AO并延长与图象的另一支有另一个交点为点C,过点A的直线l与x轴的交点为点
(m为常数)的图象上,连接AO并延长与图象的另一支有另一个交点为点C,过点A的直线l与x轴的交点为点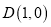 ,过点C作CE∥x轴交直线l于点E.
,过点C作CE∥x轴交直线l于点E.
(1)求m的值,并求直线l对应的函数解析式;
(2)求点E的坐标;
(3)过点B作射线BN∥x轴,与AE交于点M (补全图形),求证: 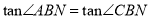
查看答案和解析>>
科目: 来源:江西省2018届九年级上学期第四次月考数学试卷 题型:解答题
已知:如图①,在平行四边形ABCD中,AB=3cm,BC=5cm,AC⊥AB.△ACD沿AC的方向匀速平移得到△PNM,速度为1cm/s;同时,点Q从点C出发,沿着CB方向匀速移动,速度为1cm/s;当△PNM停止平移时,点Q也停止移动,如图②.设移动时间为t(s)(0<t<4).连接PQ、MQ、MC.解答下列问题:
(1)当t为何值时,PQ∥AB?
(2)当t=3时,求△QMC的面积;
(3)是否存在某一时刻t,使PQ⊥MQ?若存在,求出t的值;若不存在,请说明理由

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com