
科目: 来源:人教版九年级上册 22.3 二次函数的应用 同步测试 题型:单选题
小敏在某次投篮中,球的运动路线是抛物线y=﹣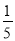 x2+3.5的一部分(如图),若命中篮圈中心,则他与篮底的距离L是( )
x2+3.5的一部分(如图),若命中篮圈中心,则他与篮底的距离L是( )
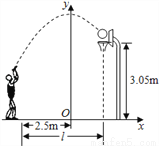
A. 3.5m B. 4m C. 4.5m D. 4.6m
B 【解析】试题分析:如图,把C点纵坐标y=3.05代入y=x2+3.5中得: x=±1.5(舍去负值), 即OB=1.5, 所以L=AB=2.5+1.5=4米,故选B.查看答案和解析>>
科目: 来源:人教版九年级上册 22.3 二次函数的应用 同步测试 题型:单选题
某公园草坪的防护栏由100段形状相同的抛物线形构件组成,为了牢固起见,每段护栏需要间距0.4m加设一根不锈钢的支柱,防护栏的最高点距底部0.5m(如图),则这条防护栏需要不锈钢支柱的总长度至少为( )
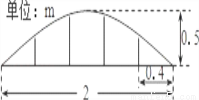
A. 50m B. 100m C. 160m D. 200m
C 【解析】分析:根据所建坐标系特点可设解析式为y=ax2+c的形式,结合图象易求B点和C点坐标,代入解析式解方程组求出a,c的值得解析式;再根据对称性求B3、B4的纵坐标后再求出总长度. 解答:【解析】 (1)由题意得B(0,0.5)、C(1,0) 设抛物线的解析式为:y=ax2+c 代入得 a=-c= ∴解析式为:y=-x2+ (2)当x=0.2时y=...查看答案和解析>>
科目: 来源:人教版九年级上册 22.3 二次函数的应用 同步测试 题型:单选题
某商品现在的售价为每件60元,每星期可卖出300件.市场调查反映,如果调整商品售价,每降价1元,每星期可多卖出20件.设每件商品降价x元后,每星期售出商品的总销售额为y元,则y与x的关系式为( )
A. y=60(300+20x) B. y=(60﹣x)(300+20x)
C. y=300(60﹣20x) D. y=(60﹣x)(300﹣20x)
B 【解析】每件商品降价x元后,则每星期的销售量为(300+20x)件,单价为(60-x)元,则y=(60-x)(300+20x),故选B.查看答案和解析>>
科目: 来源:人教版九年级上册 22.3 二次函数的应用 同步测试 题型:单选题
如图,点E、F、G、H分别是正方形ABCD边AB、BC、CD、DA上的点,且AE=BF=CG=DH.设A、E两点间的距离为x,四边形EFGH的面积为y,则y与x的函数图象可能为( )
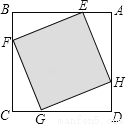
A. 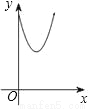 B.
B. 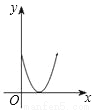 C.
C. 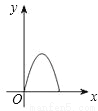 D.
D. 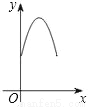
查看答案和解析>>
科目: 来源:人教版九年级上册 22.3 二次函数的应用 同步测试 题型:单选题
便民商店经营一种商品,在销售过程中,发现一周利润y(元)与每件销售价x(元)之间的关系满足y=-2(x-20)2+1558,由于某种原因,价格只能15≤x≤22,那么一周可获得最大利润是( )
A.20 B.1508 C.1550 D.1558
D. 【解析】 试题分析:∵一周利润y(元)与每件销售价x(元)之间的关系满足y=-2(x-20)2+1558,且15≤x≤22, ∴当x=20时,y最大值=1558. 故选D.查看答案和解析>>
科目: 来源:人教版九年级上册 22.3 二次函数的应用 同步测试 题型:单选题
用长为6m的铝合金型材做一个形状如图所示的矩形窗框,要使做成的窗框的透光面积最大,则该窗的长,宽应分别做成( )

A. 1.5m,1m B. 1m,0.5m C. 2m,1m D. 2m,0.5m
A 【解析】试题分析:设长为x,则宽为,S=,即S=, 要使做成的窗框的透光面积最大,则x=,于是宽为=1m, 所以要使做成的窗框的透光面积最大,则该窗的长,宽应分别做成1.5m,1m,故选A.查看答案和解析>>
科目: 来源:人教版九年级上册 22.3 二次函数的应用 同步测试 题型:单选题
图(1)是一个横断面为抛物线形状的拱桥,拱顶(拱桥洞的最高点)离水面2m,水面宽4m.如图(2)建立平面直角坐标系,则抛物线的关系式是( )
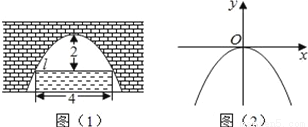
A. y=﹣2x2 B. y=2x2 C. y=﹣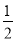 x2 D. y=
x2 D. y=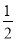 x2
x2
查看答案和解析>>
科目: 来源:人教版九年级上册 22.3 二次函数的应用 同步测试 题型:单选题
下列图形中,阴影部分的面积为2的有( )个.
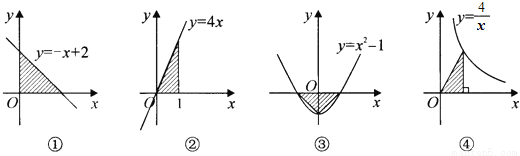
A. 4个 B. 3个 C. 2个 D. 1个
B 【解析】①y=-x+2,当x=0,y=2,当y=0,x=2,∴S阴影部分=12×2×2=2; ②y=4x,当x=1,y=4,∴S阴影部分=12×1×4=2; ③y=x2-1,当x=0,y=-1,当y=0,x=±1, S阴影部分=12×1×2=1; ④y=4x,∴xy=4,∴S阴影部分=12×4=2;故阴影部分的面积为2的有 ①②④.故选B.查看答案和解析>>
科目: 来源:人教版九年级上册 22.3 二次函数的应用 同步测试 题型:解答题
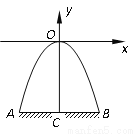
如图,某隧道口的横截面是抛物线形,已知路宽AB为6米,最高点离地面的距离OC为5米.以最高点O为坐标原点,抛物线的对称轴为y轴,1米为数轴的单位长度,建立平面直角坐标系,求:(1)以这一部分抛物线为图象的函数解析式,并写出x的取值范围;(2)有一辆宽2.8米,高1米的农用货车(货物最高处与地面AB的距离)能否通过此隧道?
查看答案和解析>>
科目: 来源:人教版九年级上册 22.3 二次函数的应用 同步测试 题型:解答题
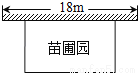
某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边由长为30米的篱笆围成.已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边长为x米.
(1)若苗圃园的面积为72平方米,求x;
(2)若平行于墙的一边长不小于8米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值;如果没有,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com