
科目: 来源:人教版九年级上册数学 22.3实际问题与二次函数(3)测试 题型:填空题
某纸箱厂第1年的利润为50万元,如果每一年比上一年的利润增长率相同,都是x,则第3年的利润为____万元。
50(1+x)2 【解析】试题分析:根据题意可知:第2年的利润为:50(1+x)万元,第3年的利润为:50(1+x)(1+x)= 万元.查看答案和解析>>
科目: 来源:人教版九年级上册数学 22.3实际问题与二次函数(3)测试 题型:填空题
用20cm长的铁丝围成一个圆,则圆的面积是____.(结果不取近似值)
cm2 【解析】试题分析:根据题意可得:2πr=20,则r=cm,则S= .查看答案和解析>>
科目: 来源:人教版九年级上册数学 22.3实际问题与二次函数(3)测试 题型:填空题
抛物线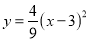 与x轴的交点为A,与y轴的交点为B,则三角形AOB的面积为____。
与x轴的交点为A,与y轴的交点为B,则三角形AOB的面积为____。
查看答案和解析>>
科目: 来源:人教版九年级上册数学 22.3实际问题与二次函数(3)测试 题型:填空题
两个数的和为6,这两个数的积最大可以达到____。
9 【解析】试题分析:设其中一个数为x,则另一个数为(6-x),则x(6-x)= ,则这两个数的积最大可以达到9.查看答案和解析>>
科目: 来源:人教版九年级上册数学 22.3实际问题与二次函数(3)测试 题型:填空题
红光旅行社有100张床位,每床每日收费10元,客床可全部租出,若每床每日收费提高2元,则租出床位减少10张,若每床每日收费再提高2元,则租出床位再减少10张,以每提高2元的这种变化方法变化下去,每床每日提高____元可获最大利润。
4元或6元 【解析】试题分析:设每床每日提高x元,每日利润为W,则W=(10+x)(100-5x)= ,根据函数解析式可知:当提高5元时,利润最大,但是每次提高都是2元,则每日提高4元或6元时可以获得最大利润.查看答案和解析>>
科目: 来源:人教版九年级上册数学 22.3实际问题与二次函数(3)测试 题型:解答题
如图4所示,一座抛物线型拱桥,桥下水面宽度是4m,拱高是2m,当水面下降1m后,水面宽度是多少?(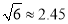 ,结果保留0.1m)
,结果保留0.1m)
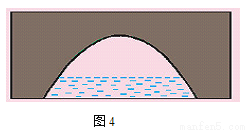
查看答案和解析>>
科目: 来源:人教版九年级上册数学 22.3实际问题与二次函数(3)测试 题型:解答题
当路况良好时,在干燥的路面上,汽车的刹车距离s与车速v之间的关系如下表所示:
v/(km/h) | 40 | 60 | 80 | 100 | 120 |
s/m | 2 | 4.2 | 7.2 | 11 | 15.6 |
(1)在平面直角坐标系中描出每对(v,s)所对应的点,并用光滑的曲线顺次连接各点。
(2)利用图象验证刹车距离s(m)与车速v(km/h)是否有如下关系: 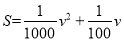 。
。
(3)求当s=9m时的车速v。
(1)图像见解析(2)符合(3)v=90km/h 【解析】试题分析:(1)、利用描点法画出函数图像;(2)、分别取几个不同的x的值代入函数解析式,看y的值是否与题目中的完全相同,如果完全相同就符合,如果有一个不相同就不符合;(3)、将s=9代入函数解析式求出v的值. 试题解析:(1)、 (2)、当v=60,s=4.2;当v=80,s=7.2;当v=100,s=11; 当v=...查看答案和解析>>
科目: 来源:人教版九年级上册数学 22.3实际问题与二次函数(3)测试 题型:解答题
张强在一次投掷铅球时,刚出手时铅球离地面 m,铅球运行的水平距离为4m时,达到最高,高度为3m,如图5所示:
m,铅球运行的水平距离为4m时,达到最高,高度为3m,如图5所示:
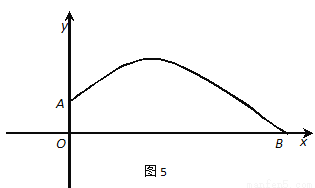
(1)请确定这个抛物线的顶点坐标
(2)求抛物线的函数关系式
(3)张强这次投掷成绩大约是多少?
(1)(4,3)(2)(3)张强这次投掷的成绩大约是10米 【解析】试题分析:(1)、根据水平距离和最大高度得出函数的顶点坐标;(2)、利用顶点和(0, 求出二次函数解析式;(3)、求出当y=0时x的值,从而得出成绩. 试题解析:(1)、(4,3); (2)、设抛物线的函数关系式为: , 因为顶点坐标为(4,3),所以有, 又因为点(0, 在抛物线上,所以有, ...查看答案和解析>>
科目: 来源:人教版九年级上册数学 22.3实际问题与二次函数(3)测试 题型:解答题
某公司生产某种产品,每件产品成本是3元,售价是4元,年销售量为10万件,为了获得更好的效益,公司准备拿出一定的资金做广告.根据经验,每年投入的广告费是x(万元)时,产品的年销售量将是原销售量的y倍,且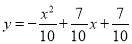 ,如果把利润看作是销售总额减去成本费和广告费,进货都能销售完,试写出年利润S(万元)与广告费x(万元)的函数关系式,并计算广告费是多少万元时,公司获得的年利润最大,最大年利润是是多少万元?
,如果把利润看作是销售总额减去成本费和广告费,进货都能销售完,试写出年利润S(万元)与广告费x(万元)的函数关系式,并计算广告费是多少万元时,公司获得的年利润最大,最大年利润是是多少万元?
查看答案和解析>>
科目: 来源:人教版九年级上册数学 22.3实际问题与二次函数(3)测试 题型:解答题
已知AB=2,C是AB上一点,四边形ACDE和四边形CBFG,都是正方形,设BC=x,
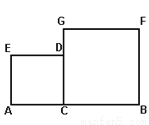
(1)AC=______;
(2)设正方形ACDE和四边形CBFG的总面积为S,用x表示S的函数解析式为S=_____.
(3)总面积S有最大值还是最小值?这个最大值或最小值是多少?
(4)总面积S取最大值或最小值时,点C在AB的什么位置?
(1)AC=2-x(0≤x≤2)(2)S=2+2(3)4(4)当x=1时,C点恰好在AB的中点上;当x=0时,C点恰好在B处;当x=2时,C点恰好在A处 【解析】试题分析:(1)、根据AB=2得出AC的长度;(2)、根据总面积等于两个正方形的面积之和得出函数解析式;(3)、根据二次函数的增减性得出面积的最大值和最小值;(4)、根据最值时x的值得出AC的长度,从而得出点C的位置. 试题解...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com