
科目: 来源:人教版九年级上册数学 22.1.4二次函数yax2+bx+c的图象和性质(1)测试 题型:填空题
若二次函数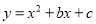 的图象经过点(-1,0),(1,-2),当
的图象经过点(-1,0),(1,-2),当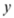 随
随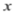 的增大而增大时,
的增大而增大时,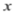 的取值范围是____________。
的取值范围是____________。
查看答案和解析>>
科目: 来源:人教版九年级上册数学 22.1.4二次函数yax2+bx+c的图象和性质(1)测试 题型:填空题
把抛物线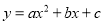 先向右平移3个单位,再向下平移2个单位,所得抛物线解析式为
先向右平移3个单位,再向下平移2个单位,所得抛物线解析式为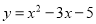 ,则a+b+c=___________。
,则a+b+c=___________。
查看答案和解析>>
科目: 来源:人教版九年级上册数学 22.1.4二次函数yax2+bx+c的图象和性质(1)测试 题型:填空题
在平面直角坐标系中,若将抛物线y=2x2-4x+3先向右平移3个单位长度,再向上平移2个单位长度,则经过这两次平移后所得抛物线的顶点坐标是__________。
(4,3) 【解析】抛物线y=2x2-4x+3=2(x2-2x+1)+1=2(x-1)2+1, 根据平移规律可得平移后解析式为y=2(x-1-3)2+1+2=2(x-4)2+3, 此时抛物线顶点坐标为(4,3). 故答案为(4,3).查看答案和解析>>
科目: 来源:人教版九年级上册数学 22.1.4二次函数yax2+bx+c的图象和性质(1)测试 题型:填空题
抛物线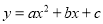 (a>0)的对称轴为直线x=1,且经过点(—1,y1),(2,y2)则试比较y1与y2的大小:y1__________y2(填“>”“<”或“=”)。
(a>0)的对称轴为直线x=1,且经过点(—1,y1),(2,y2)则试比较y1与y2的大小:y1__________y2(填“>”“<”或“=”)。
查看答案和解析>>
科目: 来源:人教版九年级上册数学 22.1.4二次函数yax2+bx+c的图象和性质(1)测试 题型:填空题
已知二次函数y=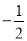 x2-7x+
x2-7x+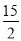 ,若自变量x分别取x1,x2,x3,且0<x1<x2<x3,则对应的函数值y1,y2,y3的大小关系是__________________(用“<”连接)。
,若自变量x分别取x1,x2,x3,且0<x1<x2<x3,则对应的函数值y1,y2,y3的大小关系是__________________(用“<”连接)。
查看答案和解析>>
科目: 来源:人教版九年级上册数学 22.1.4二次函数yax2+bx+c的图象和性质(1)测试 题型:填空题
二次函数y=x2-2x-3的图象关于原点O(0,0)对称的图象的解析式是_________.
Y=_-x2-2x+3(写成顶点式也对) 【解析】利用抛物线的性质. 【解析】 可先从抛物线y=x2-2x-3上找三个点(0,-3),(1,-4),(-1,0).它们关于原点对称的点是(0,3),(-1,4),(1,0).可设新函数的解析式为y=ax2+bx+c,则c=3,a-b+c=4,a+b+c=0.解得a=-1,b=-2,c=3.故所求解析式为:y=-x2-2x+3. ...查看答案和解析>>
科目: 来源:人教版九年级上册数学 22.1.4二次函数yax2+bx+c的图象和性质(1)测试 题型:填空题
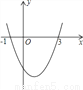
已知二次函数y=ax2+bx+c的图象如图所示,它与x轴的两个交点分别为(-1,0),(3,0).对于下列命题:①b-2a=0;②abc<0;③a-2b+4c<0;④8a+c>0.其中正确的有____________。
查看答案和解析>>
科目: 来源:人教版九年级上册数学 22.1.4二次函数yax2+bx+c的图象和性质(1)测试 题型:解答题
已知抛物线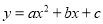 的对称轴为x=2,且经过点(1,4)和(5,0),试求该抛物线的表达式。
的对称轴为x=2,且经过点(1,4)和(5,0),试求该抛物线的表达式。
查看答案和解析>>
科目: 来源:人教版九年级上册数学 22.1.4二次函数yax2+bx+c的图象和性质(1)测试 题型:解答题
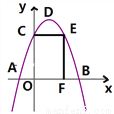
如图,抛物线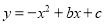 与x轴交于点A、B,与y轴交于点C,点O为坐标原点,点D为抛物线顶点,点E在抛物线上,点F在x轴上,四边形OCEF为矩形,且OF=2,EF=3
与x轴交于点A、B,与y轴交于点C,点O为坐标原点,点D为抛物线顶点,点E在抛物线上,点F在x轴上,四边形OCEF为矩形,且OF=2,EF=3
(1)求抛物线所对应的函数解析式;
(2)求ΔABC的面积。
查看答案和解析>>
科目: 来源:人教版九年级上册数学 22.1.4二次函数yax2+bx+c的图象和性质(1)测试 题型:解答题
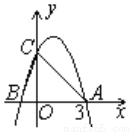
如图所示,二次函数y=-x2+2x+m的图象与x轴的一个交点为A(3,0),另一个交点为B,且与y轴交于点C.
(1)求m的值;
(2)求点B的坐标;
(3)该二次函数图象上有一点D(x,y)(其中x>0,y>0),使S△ABD=S△ABC,求点D的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com