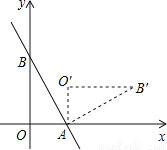
如图，直线y=﹣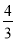x+4与x轴、y轴分别交于A、B两点，把△AOB绕点A顺时针旋转90°后得到△AO′B′，则点B′的坐标是 ．

（7，3） 【解析】 试题分析：由直线y=﹣x+4与x轴、y轴分别交于A（3，0）、B（0，4）两点，由图易知点B′的纵坐标为O′A=OA=3，横坐标为OA+O′B′=OA+OB=7．则点B′的坐标是（7，3）．

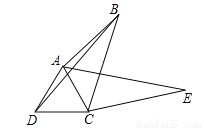
如图，在四边形ABCD中，∠ABC=30°，将△DCB绕点C顺时针旋转60°后，点D的对应点恰好与点A重合，得到△ACE，若AB=3，BC=4，则BD= （提示：可连接BE）

5． 【解析】 试题分析：连接BE，如右图所示，∵△DCB绕点C顺时针旋转60°得到△ACE，AB=3，BC=4，∠ABC=30°，∴∠BCE=60°，CB=CE，AE=BD，∴△BCE是等边三角形，∴∠CBE=60°，BE=BC=4，∴∠ABE=∠ABC+∠CBE=30°+60°=90°，∴AE===5，又∵AE=BD，∴BD=5，故答案为：5．

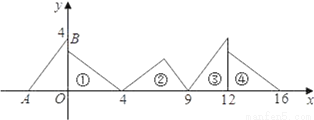
如图，在直角坐标系中，已知点A（﹣3，0），B（0，4），对△OAB连续作旋转变换，依次得到三角形①，②，③，④…，则三角形⑩的直角顶点的坐标为______．

（36，0） 【解析】试题解析：由原图到图③，相当于向右平移了12个单位长度， 三角形④的直角顶点的坐标为（12，0），象这样平移四次直角顶点是（12×4，0），即（48，0）， 则三角形⑫的直角顶点的坐标为（48，0）.

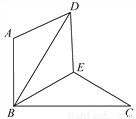
如图，△BAD是由△BEC在平面内绕点B旋转60°而得，且AB⊥BC，BE＝CE，连接DE.

（1）求证：△BDE≌△BCE；

（2）试判断四边形ABED的形状，并说明理由．

证明见解析. 【解析】试题分析：（1）根据旋转的性质可得DB=CB，∠ABD=∠EBC，∠ABE=60°，然后根据垂直可得出∠DBE=∠CBE=30°，继而可根据SAS证明△BDE≌△BCE； （2）根据（1）以及旋转的性质可得，△BDE≌△BCE≌△BDA，继而得出四条棱相等，证得四边形ABED为菱形． （1）证明：∵△BAD是由△BEC在平面内绕点B旋转60°而得， ∴...

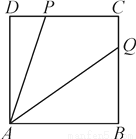
如图，P是正方形ABCD的边CD上一点，∠BAP的平分线交BC于点Q，求证：AP＝DP＋BQ.

证明见解析. 【解析】试题分析：根据旋转的性质得出∠E=∠AQB，∠EAD=∠QAB，进而得出∠PAE=∠E，即可得出AP=PE=DP+DE=DP+BQ． 试题解析：证明：将△ABQ绕A逆时针旋转90°得到△ADE，由旋转的性质可得出∠E=∠AQB，∠EAD=∠QAB，又∵∠PAE=90°﹣∠PAQ=90°﹣∠BAQ=∠DAQ=∠AQB=∠E，在△PAE中，得AP=PE=DP+DE=D...

如图，把一副三角板如图甲放置，其中∠ACB=DEC=90°，∠A=45°，∠D=30°，AB=6cm，DC=7cm．把三角板DCE绕点C顺时针旋转15°得到△D′CE′，如图乙，这时AB与CD′相交于点O，D′E′与AB、CB分别相交于点F、G，连接AD′．

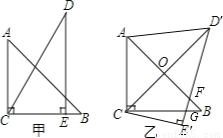
（1）求∠OFE′的度数；

（2）求线段AD′的长．

（1）120°（2）5cm 【解析】 试题分析：（1）由∠BCE′=15°，∠E′=90°，易得∠CGE′=∠FGB=75°，可得∠OFE1=∠B+∠FGB=45°+75°=120°； （2）由∠OFE′=∠120°，得∠D′FO=60°，所以∠D′OF=90°，由AC=BC，AB=6cm，得OA=OB=OC=3cm，所以，OD′=CD′﹣OC=7﹣3=4cm，在Rt△AD′O中...

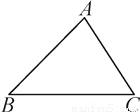
如图，在△ABC中，∠B＝45°，∠C＝60°，将△ABC绕点A旋转30°后得到△AB1C1，求∠BAC1的度数．

105°. 【解析】试题分析：分两种情况：①顺时针旋转30°；②逆时针旋转30°． 试题解析：【解析】 分两种情况：①顺时针旋转30°，如图1； ∵∠B＝45°，∠C＝60°，∴∠A=180°-∠B-∠C=75°． ∠BAC1＝∠BAC-∠CAC1＝75°-30°=45°． ②逆时针旋转30°，如图2． ∠BAC1＝∠BAC+∠CAC1＝75°+30°=105...

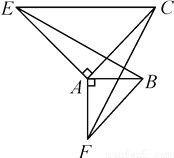
如图，已知△ACE，△ABF都是等腰直角三角形，且∠BAF＝∠CAE＝90°.那么你能利用旋转的知识说明FC＝BE吗？

理由见解析. 【解析】试题分析：由AE，AB绕A点顺时针旋转90°分别与AC，AF重合，得到△AFC可看作是△ABE绕A点顺时针旋转90°得到的，从而得到结论． 试题解析：【解析】 ∵AE，AB绕A点顺时针旋转90°分别与AC，AF重合，∴△AFC可看作是△ABE绕A点顺时针旋转90°得到的，∴FC＝BE．

如图，把△AOB绕点O逆时针旋转40°可得到△A′OB′.

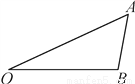
(1)画出旋转后的图形；

(2)指出旋转角的度数并找出一组对应边．

(1)图形见解析； (2)旋转角∠AOA′＝∠BOB′＝40°，OA，OA′或OB，OB′或AB，A′B′是一组对应边. 【解析】试题分析：（1）作出△AOB绕点O逆时针旋转40°后的图形△A′OB′即可； （2）根据A和A′，B和B′O和O是对应点，得出旋转角和对应边即可． 试题解析：【解析】 （1）作图如下： (2)旋转角∠AOA′＝∠BOB′＝40°，OA，O...

抛物线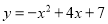的顶点坐标为（ ）

A. （-2,3） B. （2,11） C. （-2,7） D. （2，-3）

B 【解析】y=-x2+4x+7=-(x2-4x+4)+11=-(x-2)2+11, 故顶点坐标为（2，11）. 故选B．