如图，正方形ABCD的边BC在等腰直角三角形PQR的底边QR上，其余两个顶点A、D分别在PQ、PR上，则PA∶AQ＝（　）．

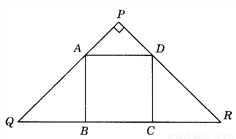
A. 1∶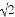 B. 1∶2 C. 1∶3 D. 2∶3

C 【解析】试题分析：四边形ABCD是正方形ABCD，则△PAD、△ABQ、△CDR是等腰直角三角形，则△PAD∽△PQR，利用比例线段可求PA：PQ（可假设正方形的边长等于a，便于计算）． ∵四边形ABCD是正方形， ∴△PAD、△ABQ、△CDR是等腰直角三角形 ∴△PAD∽△PQR ∴PA：PQ=AD：QR 设正方形ABCD的边长是a，则AD=a，BQ=C...

如图，△ABC中，AB=AC=18，BC=12，正方形DEFG的顶点E，F在△ABC内，顶点D，G分别在AB，AC上，AD=AG，DG=6，则点F到BC的距离为．

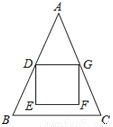
A. 1 B. 2 C. 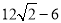D.

D 【解析】试题分析：过点A作BC的垂线得出高线为12，根据相似三角形的性质可得点A到DG的距离为6，则点F到BC的距离为：6－6.

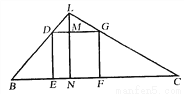
如图，光源L距地面（LN）8m，距正方体大箱顶站（LM）2m，已知，在光源照射下，箱子在左侧的影子BE长5m，求箱子在右侧的影子CF的长．（箱子边长为6m）

13 【解析】【试题分析】由题意得，箱子的棱长为8-2=6，根据△BDE∽BLN得，=， 即=，再计算NF=6-=，最后根据△CFG∽△CNL得，=，即=，得解CF=13； 【试题解析】 由△BDE∽BLN得，=， 即=， 解得EN=， 所以，NF=6-=， 由△CFG∽△CNL得，=， 即=， 解得CF=13；

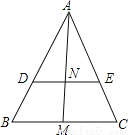
如图，在△ABC中，DE∥BC，△ABC的高AM交DE于点N，BC=15，AM=10，DE=MN，求MN的长．

6 【解析】 试题分析：设MN=x，则AN=10﹣x，由平行线分线段成比例定理得出比例式，即可得出MN的长． 【解析】 设MN=x，则AN=10﹣x， ∵DE∥BC， ∴， 即， 即MN的长为6．

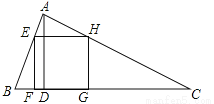
（2016湖南省怀化市）如图，△ABC为锐角三角形，AD是BC边上的高，正方形EFGH的一边FG在BC上，顶点E、H分别在AB、AC上，已知BC=40cm，AD=30cm．

（1）求证：△AEH∽△ABC；

（2）求这个正方形的边长与面积．

（1）证明见解析；（2）边长为cm，面积为cm2． 【解析】试题分析：（1）由正方形可得EH∥BC，所以可以得到对应的两组角相等，即可证明相似；（2）设正方形边长为x，再由△AEH∽△ABC得到对应边成比例，列出关于x的方程，解出x即可． 试题解析： (1)证明：∵四边形EFGH是正方形，∴EH∥BC，∴∠AEH＝∠B，∠AHE＝∠C，∴△AEH∽△ABC； (2)【解析】...

以下列各组数据为边长作三角形，其中能组成直角三角形的是（ ）.

A. 3，5，3 B. 4，6，8 C. 7，24，25 D. 6，12，13

C 【解析】试题分析：欲求证是否为直角三角形，这里给出三边的长，只要满足勾股定理的逆定理即可．A、；B、；C、；D、．根据勾股定理7，24，25能组成直角三角形. 故选：C．

一个直角三角形的两直角边长分别为3和4，那么它斜边上的高线长为（ ）

A. 5 B. 2.5 C. 2.4 D. 2

C 【解析】试题分析：根据勾股定理可得：三角形的斜边长为5，则根据面积相等的法则可得：×3×4=×5h，则h=2.4，即斜边上的高线长为2.4

如图是一张直角三角形的纸片，两直角边AC=6cm、BC=8cm，现将△ABC折叠，使点B与点A重合，折痕为DE，则BE的长为（ ）

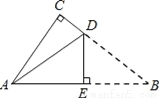
A. 4cm B. 5cm C. 6cm D. 10cm

B 【解析】试题分析：先根据勾股定理求出AB的长，再由图形折叠的性质可知，AE=BE，故可得出结论． ∵△ABC是直角三角形，两直角边AC=6cm、BC=8cm， ∴AB===10cm， ∵△ADE由△BDE折叠而成， ∴AE=BE=AB=×10=5cm．

如图所示，一圆柱高8cm，底面半径为2cm，一只蚂蚁从点A爬到点B处吃食，要爬行的最短路程（π取3）是（ ）

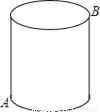
A. 20cm B. 10cm C. 14cm D. 无法确定

B 【解析】试题分析：先将图形展开，根据两点之间，线段最短，利用根据勾股定理即可得出结论． 如图所示：沿AC将圆柱的侧面展开， ∵底面半径为2cm， ∴BC==2π≈6cm， 在Rt△ABC中， ∵AC=8cm，BC=6cm， ∴AB===10cm．

如图，在△ABC中，AC=10，DC=6，AD=8，BC=21，则AB的长为（ ）.

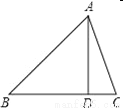
A. 15 B. 16 C. 14 D. 17

D 【解析】试题分析：先根据勾股定理的逆定理判断出△ADC的形状，再由勾股定理即可得出结论．∵AC=10，DC=6，AD=8，，∴△ADC是直角三角形，∴AD⊥BC，∴∠ADB=90°．在Rt△ABD中，∵AD=8，BD=BC﹣DC=21﹣6=15，∴AB==17． 故选：D．