
科目: 来源:人教版九年级上册数学 21.2.1配方法(1)练习 题型:填空题
对于方程x2=m-1,若方程有两个不相等的实数根,则m______;若方程有两个相等的实数根,则m______;若方程无实数根,则m______.
>1 =1 <1 【解析】若方程有两个不相等的实数根,则x2>0,所以m-1>0,则m>1; 若方程有两个相等的实数根,则x2=0,所以m-1=0,则m=1; 若方程无实数根,则x2<0,所以m-1<0,则m<1. 故答案为(1)>1;(2)=1;(3)<1.查看答案和解析>>
科目: 来源:人教版九年级上册数学 21.2.1配方法(1)练习 题型:解答题
用直接开平方法解方程:
(1) 9x2=25;
(2) x2-144=0.
(1) x1=,x2=- (2) x1=12,x2=-12 【解析】试题分析: (1)系数化为1后,直接开平方求解; (2)先把常数项移到等号的右边,再用直接开平方法求解. 试题解析: (1) 【解析】 9x2=25,x2=,所以x1=,x2=- (2) 【解析】 x2-144=0,x2=144,所以x1=12,x2=-12.查看答案和解析>>
科目: 来源:人教版九年级上册数学 21.2.1配方法(1)练习 题型:单选题
一元二次方程(x+6)2=16可化为两个一元一次方程,其中一个一元一次方程是x+6=4,则另一个一元一次方程是( )
A. x-6=4 B. x-6=-4 C. x+6=4 D. x+6=-4
D 【解析】(x+6)2=16,直接开平方得x+6=±4,即x+6=4或x+6=-4. 故选D.查看答案和解析>>
科目: 来源:人教版九年级上册数学 21.2.1配方法(1)练习 题型:单选题
一元二次方程(x+6)2-9=0的根是( )
A. x1=6,x2=-6 B. x1=x2=-6 C. x1=-3,x2=-9 D. x1=3,x2=-9
C 【解析】(x+6)2-9=0,移项得(x+6)2=9,直接开平方得x+6=±3,所以x1=-3,x2=-9. 故选C.查看答案和解析>>
科目: 来源:人教版九年级上册数学 21.2.1配方法(1)练习 题型:单选题
已知b<0,关于x的一元二次方程(x-1)2=b的根的情况是( )
A. 有两个不相等的实数根 B. 有两个相等的实数根
C. 没有实数根 D. 有两个实数根
C 【解析】试题分析:∵(x﹣1)2≥0,而b<0, ∴(x﹣1)2=b没有实数根. 故选C.查看答案和解析>>
科目: 来源:人教版九年级上册数学 21.2.1配方法(1)练习 题型:填空题
方程(x-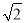 )2=2的解是______________________,方程2(x+1)2-8=0的解是____________________.
)2=2的解是______________________,方程2(x+1)2-8=0的解是____________________.
查看答案和解析>>
科目: 来源:人教版九年级上册数学 21.2.1配方法(1)练习 题型:填空题
若方程(x-a)2=b的解是x1=1,x2=3,则a=____,b=____.
2 1 【解析】根据题意得解得a=2,b=1. 故答案为(1). 2;(2). 1.查看答案和解析>>
科目: 来源:人教版九年级上册数学 21.2.1配方法(1)练习 题型:解答题
用直接开平方法解方程:
(1) (x-3)2-9=0;
(2) (2t-1)2=16.
(1) x1=0,x2=6 (2) 【解析】 t1=,t2=- 【解析】试题分析: (1)先移项,再用直接开平方法求解; (2)用直接开平方法求解. 试题解析: (1) (x-3)2-9=0,移项得(x-3)2=9,直接开平方得x-3=±3,所以x1=0,x2=6; (2) (2t-1)2=16,直接开平方得2t-1=±4,所以t1=,t2=-.查看答案和解析>>
科目: 来源:人教版九年级上册数学 21.2.1配方法(1)练习 题型:单选题
x1,x2是一元二次方程3(x-1)2=15的两个解,且x1<x2,下列说法正确的是( )
A. x1小于-1,x2大于3 B. x1小于-2,x2大于3
C. x1,x2在-1和3之间 D. x1,x2都小于3
A 【解析】试题分析:∵x1、x2是一元二次方程3(x﹣1)2=15的两个解,且x1<x2,∴(x﹣1)2=5,∴x﹣1=±,∴x2=1+>3,x1=1﹣<﹣1. 故选:A.查看答案和解析>>
科目: 来源:人教版九年级上册数学 21.2.1配方法(1)练习 题型:单选题
给出一种运算:对于函数y=xn,规定y′=nxn-1.例如:若函数y=x4,则有y′=4x3.已知函数y=x3,则方程y′=12的解是( )
A. x1=4,x2=-4 B. x1=2,x2=-2 C. x1=x2=0 D. x1=2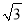 ,x2=-2
,x2=-2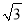
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com