
科目: 来源:人教版九年级上册数学 24.4弧长和扇形面积(2)练习 题型:单选题
若圆锥的侧面展开图是一个半径为a的半圆,则圆锥的高为( )
A. a B. 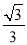 a C. 3a D.
a C. 3a D. 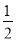 a
a
查看答案和解析>>
科目: 来源:人教版九年级上册数学 24.4弧长和扇形面积(2)练习 题型:填空题
用一张半径为9 cm、圆心角为120°的扇形纸片,做成一个圆锥形冰淇淋的侧面(不计接缝),那么这个圆锥形冰淇淋的底面半径是_________ cm.
3 【解析】【解析】 半径为9cm、圆心角为120°的扇形弧长是: 设圆锥的底面半径是r, 则2πr=6π, 解得:r=3cm. 这个圆锥形冰淇淋的底面半径是3cm.查看答案和解析>>
科目: 来源:人教版九年级上册数学 24.4弧长和扇形面积(2)练习 题型:填空题
如图,已知圆锥的母线长OA=8,地面圆的半径r=2.若一只小虫从A点出发,绕圆锥的侧面爬行一周后又回到A点,则小虫爬行的最短路线的长是_________(结果保留根式).
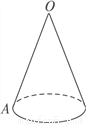
查看答案和解析>>
科目: 来源:人教版九年级上册数学 24.4弧长和扇形面积(2)练习 题型:解答题
一个圆锥的高为3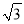 cm,侧面展开图是半圆,
cm,侧面展开图是半圆,
求:(1)圆锥母线与底面半径的比;
(2)锥角的大小;
(3)圆锥的全面积.
(1)2;(2)60°;(3)27π. 【解析】试题分析:(1)根据展开图是半圆,可求得母线与半径比值. (2)利用结论(1)可知锥角大小. (3)由(2)结论,利用特殊三角形计算出底面半径和母线长,分别求出侧面积和底面积. 试题解析: 如图,AO为圆锥的高,经过AO的截面是等腰△ABC,则AB为圆锥母线l,BO为底面半径r. (1)因圆锥的侧面展开图是半圆,所...查看答案和解析>>
科目: 来源:人教版九年级上册数学 24.4弧长和扇形面积(2)练习 题型:填空题
已知圆锥的母线与高的夹角为30°,母线长为4 cm,则它的侧面积为_________ cm2(结果保留π).
8π 【解析】由题意知,底面半径是2,则底面周长是4π,所以侧面积是.查看答案和解析>>
科目: 来源:人教版九年级上册数学 24.4弧长和扇形面积(2)练习 题型:填空题
如图,有一圆锥形粮堆,其主视图是边长为6 m的正三角形ABC,母线AC的中点P处有一老鼠正在偷吃粮食,小猫从B处沿圆锥表面去偷袭老鼠,则小猫经过的最短路程是___________ m.(结果不取近似数)
查看答案和解析>>
科目: 来源:人教版九年级上册数学 24.4弧长和扇形面积(2)练习 题型:填空题
若圆锥的底面直径为6 cm,母线长为5 cm,则它的侧面积为___________.(结果保留π)
15π cm2 【解析】试题解析:这个圆锥的底面直径是 圆锥侧面展开扇形的面积: 故答案为:查看答案和解析>>
科目: 来源:人教版九年级上册数学 24.4弧长和扇形面积(2)练习 题型:单选题
在Rt△ABC中,已知AB=6,AC=8,∠A=90°.如果把Rt△ABC绕直线AC旋转一周得到一个圆锥,其全面积为S1;把Rt△ABC绕直线AB旋转一周得到另一个圆锥,其全面积为S2.那么S1∶S2等于( )
A. 2∶3 B. 3∶4 C. 4∶9 D. 5∶12
A 【解析】试题解析: 绕直线旋转一周得到一个圆锥,全面积 绕直线旋转一周得到一个圆锥,全面积 故选A.查看答案和解析>>
科目: 来源:人教版九年级上册数学 24.4弧长和扇形面积(2)练习 题型:填空题
如图,是小芳学习时使用的圆锥形台灯灯罩的示意图,则围成这个灯罩的铁皮的面积为____________ cm2(不考虑接缝等因素,计算结果用π表示).
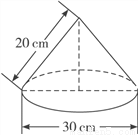
查看答案和解析>>
科目: 来源:人教版九年级上册数学 24.4弧长和扇形面积(2)练习 题型:单选题
制作一个底面直径为30 cm、高为40 cm的圆柱形无盖铁桶,所需铁皮至少为( )
A. 1 425π cm2 B. 1 650π cm2 C. 2 100π cm2 D. 2 625π cm2
A 【解析】试题解析:这个圆柱的底面直径是 所需铁皮就是一个底面积与侧面积的和. 故选A.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com