
科目: 来源:天津市 2017-2018学年 八年级数学上册 全等三角形判定 填空题练习(含答案) 题型:填空题
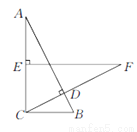
如图,在Rt△ABC中,∠ACB=90°,BC=2 cm,CD⊥AB,在AC上取一点E,使EC=BC,过点E作EF⊥AC交CD的延长线于点F,若EF=5 cm,则AE=______cm.
查看答案和解析>>
科目: 来源:天津市 2017-2018学年 八年级数学上册 全等三角形判定 填空题练习(含答案) 题型:填空题
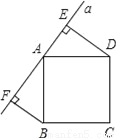
如图所示,直线a经过正方形ABCD的顶点A,分别过正方形的顶点B、D作BF⊥a于点F,DE⊥a于点E,若DE=8,BF=5,则EF的长为__.
查看答案和解析>>
科目: 来源:天津市 2017-2018学年 八年级数学上册 全等三角形判定 填空题练习(含答案) 题型:填空题
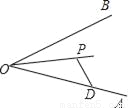
如图,已知点P为∠AOB的角平分线上的一定点,D是射线OA上的一定点,E是OB上的某一点,满足PE=PD,则∠OEP与∠ODP的数量关系是___________.
查看答案和解析>>
科目: 来源:天津市 2017-2018学年 八年级数学上册 全等三角形判定 填空题练习(含答案) 题型:填空题
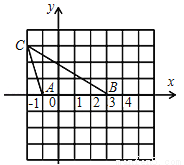
在直角坐标系中,如图有△ABC,现另有一点D满足以A、B、D为顶点的三角形与△ABC全等,则D点坐标为 .
查看答案和解析>>
科目: 来源:天津市 2017-2018学年 八年级数学上册 全等三角形判定 填空题练习(含答案) 题型:填空题
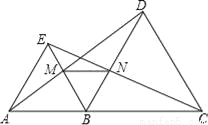
如图,△ABE,△BCD均为等边三角形,点A,B,C在同一条直线上,连接AD,EC,AD与EB相交于点M,BD与EC相交于点N,下列说法正确的有:___________
①AD=EC;②BM=BN;③MN∥AC;④EM=MB.
查看答案和解析>>
科目: 来源:人教版九年级上册数学 22.1.4二次函数yax2+bx+c的图象和性质(2)测试 题型:单选题
二次函数的图象经过(0,3),(﹣2,﹣5),(1,4)三点,则它的解析式为( )
A. y=x2+6x+3 B. y=﹣3x2﹣2x+3 C. y=2x2+8x+3 D. y=﹣x2+2x+3
D 【解析】试题分析:把三点坐标代入二次函数的解析式,即可得出二次函数的解析式. 【解析】 设二次函数的解析式为:y=ax2+bx+c, 把(0,3),(?2,?5),(1,4)代入得, 解得 , 所以二次函数的解析式为:y=?x2+2x+3, 故选:D.查看答案和解析>>
科目: 来源:人教版九年级上册数学 22.1.4二次函数yax2+bx+c的图象和性质(2)测试 题型:单选题
已知抛物线经过点(0,4),(1,﹣1),(2,4),那么它的对称轴是直线( )
A. x=﹣1 B. x=1 C. x=3 D. x=﹣3
B 【解析】试题分析:由二次函数图象的对称性即可求出对称轴. 【解析】 ∵点(0,4)与(2,4)关于抛物线对称, ∴对称轴为x=1. 故选B.查看答案和解析>>
科目: 来源:人教版九年级上册数学 22.1.4二次函数yax2+bx+c的图象和性质(2)测试 题型:单选题
抛物线y=ax2+bx+c经过点(3,0)和(2,﹣3),且以直线x=1为对称轴,则它的解析式为( )
A. y=﹣x2﹣2x﹣3 B. y=x2﹣2x﹣3 C. y=x2﹣2x+3 D. y=﹣x2+2x﹣3
B 【解析】试题分析:把已知两点坐标代入抛物线解析式,再由对称轴公式列出关系式,联立求出a,b,c的值,即可确定出解析式. 【解析】 把(3,0)与(2,?3)代入抛物线解析式得: , 由直线x=1为对称轴,得到=1,即b=?2a, 代入方程组得: , 解得:a=1,b=?2,c=?3, 则抛物线解析式为y=x2?2x?3, 故选B.查看答案和解析>>
科目: 来源:人教版九年级上册数学 22.1.4二次函数yax2+bx+c的图象和性质(2)测试 题型:单选题
下列二次函数中,图象以直线x=2为对称轴、且经过点(0,1)的是( )
A. y=(x﹣2)2+1 B. y=(x+2)2+1 C. y=(x﹣2)2﹣3 D. y=(x+2)2﹣3
C 【解析】试题分析:采用逐一排除的方法.先根据对称轴为直线x=2排除B、D,再将点(0,1)代入A、C两个抛物线解析式: 将点(0,1)代入A中,得(x﹣2)2+1=(0﹣2)2+1=5,故A选项错误, 代入C中,得(x﹣2)2﹣3=(0﹣2)2﹣3=1,故C选项正确. 故选:C.查看答案和解析>>
科目: 来源:人教版九年级上册数学 22.1.4二次函数yax2+bx+c的图象和性质(2)测试 题型:单选题
根据下表中的二次函数y=ax2+bx+c的自变量x与函数y的对应值,可判断二次函数的解析式为( )
x | … |
| 0 | 1 | 2 | … |
y | … |
|
|
|
| … |
A. y=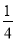 x2﹣
x2﹣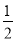 x﹣
x﹣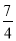 B. y=
B. y=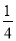 x2+
x2+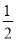 x﹣
x﹣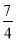
C. y=﹣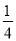 x2﹣
x2﹣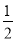 x+
x+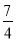 D. y=﹣
D. y=﹣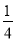 x2+
x2+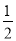 x+
x+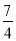
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com