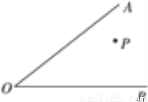
已知，如图所示，甲、乙、丙三个人做传球游戏，游戏规则如下：甲将球传给乙，乙将球立刻传给丙，然后丙又立刻将球传给甲．若甲站在∠AOB内的P点，乙站在OA上，丙站在OB上，并且甲、乙、丙三人的传球速度相同．问乙和丙必须站在何处，才能使球从甲到乙、乙到丙、最后丙到甲这一轮所用的时间最少？

见解析 【解析】试题分析：分别作出点P关于OA、OB的对称点P1、P2，连接P1P2与OA、OB的交点即为乙、丙的位置. 试题解析：如图所示，(1)分别作点P关于OA，OB的对称点P1，P2， (2)连接P1P2，与OA，OB分别相交于点M，N， 因为乙站在OA上，丙站在OB上，所以乙必须站在OA上的M处，丙必须站在OB上的N处才能使传球所用时间最少．

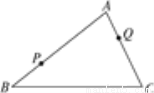
如图所示，P，Q为△ABC边上的两个定点，在BC上求作一点R，使△PQR的周长最小．

见解析 【解析】试题分析：作出点P关于BC的对称点P′，连接QP′交BC于R，那么△PQR的周长最小 试题解析：(1)作点P关于BC所在直线的对称点P′， (2)连接P′Q，交BC于点R，则点R就是所求作的点(如图所示)．

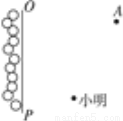
七年级(1)班同学做游戏，在活动区域边OP放了一些球(如图)，则小明按怎样的路线跑，去捡哪个位置的球，才能最快拿到球跑到目的地A?

见解析 【解析】试题分析：作出小明关于OP的对称点A′，连接AA′，与OP交点即为满足条件的点. 试题解析：如图，作小明关于活动区域边线OP的对称点A′，连接AA′交OP于点B，则小明行走的路线是小明→B→A，即在B处捡球，才能最快拿到球跑到目的地A.

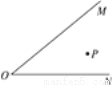
公园内两条小河MO，NO在O处汇合，两河形成的半岛上有一处景点P(如图所示)．现计划在两条小河上各建一座小桥Q和R，并在半岛上修三段小路，连通两座小桥与景点，这两座小桥应建在何处才能使修路费用最少？请说明理由．

见解析 【解析】试题分析：可过点P分别作关于OM，ON的对称点P′，P″，连接P′P″，与OM、ON的交点即为满足条件的建桥地点. 试题解析：如图，作P关于OM的对称点P′，作P关于ON的对称点P″，连接P′P″，分别交MO，NO于Q，R，连接PQ，PR，则P′Q＝PQ，PR＝P″R，则Q，R就是小桥所在的位置． 理由：在OM上任取一个异于Q的点Q′，在ON上任取一个异于R的点R...

如图，牧童在A处放牛,其家在B处,A、B到河岸的距离分别为AC、BD,且AC=BD。若A到河岸CD的中点的距离为500米.

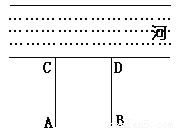
（1）牧童从A处放牛牵到河边饮水后再回家,试问在何处饮水,所走路程最短? 用尺规作图在图中画出来

（2）最短路程是多少?

（1）作图见解析； （2）1000米． 【解析】 试题分析：作出点A关于河岸l的对称点A′，连接A′B，交河岸l于点D，则点D是牛饮水的位置．分析：根据轴对称的性质和“两点之间线段最短”，连接A′B，得到最短距离为A′B，再根据相似三角形的性质和A到河岸CD的中点的距离为500米，即可求出A'B的值． 试题解析：（1）作出A的对称点A′，连接A′B与CD相交于M，则牧童从A处把牛...

如图所示,在△ABC中,BC=AC,BE=AE,则由“SSS”可以判定( )

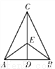
A. △ACD≌△BCD B. △ADE≌△BDE C. △ACE≌△BCE D. 以上都对

C 【解析】试题分析：三条边对应相等，BC=AC,BE=AE,CE=CE.所以△ACE≌△BCE，故选C.

如图,AB=AD,CB=CD,∠B=30°,∠BAD=46°,则∠ACD的度数是( )

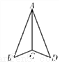
A. 120° B. 125° C. 127° D. 104°

C 【解析】试题分析：AB=AD,CB=CD,AC=AC所以∆ABC?∆ACD,所以∠B=∠D=30°,因为∠BAD=46°，所以∠CAD=23°，所以∠ACD=180°-30°-23°=127°，故选C.

已知△ABC的三边分别为a,b,c,△A'B'C'的三边分别为a',b',c',且有a2+a'2+b2+b'2+c2+c'2=2ab'+2bc'+2ca',则△ABC与△A'B'C'( )

A. 一定全等 B. 不一定全等 C. 一定不全等 D. 无法确定

A 【解析】试题分析：a2+a'2+b2+b'2+c2+c'2=2ab'+2bc'+2ca',所以a2+b'2-2ab' +b2 +c'2-2bc'+c2+a'2 -2ca'=0，（a- b'）2+（b- c'）2+（c- a'）2=0，所以a-=b'，b=c'，c= a'，所以△ABC与△A'B'C'一定全等.故选A.

若AD=BC,∠A=∠B,直接能利用“SAS”证明△ADF≌△BCE的条件是( )

A. AE=BF B. DF=CE C. AF=BE D. ∠CEB=∠DFA

C 【解析】试题分析：用边角边证明两三角形全等，已知其中一个对应角相等和一条对应边相等，则还需要的条件是相等角的另外一条临边相等，即AF=BE，故选C.

如图,其中全等的三角形是( )

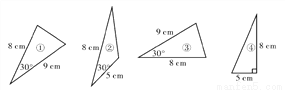
A. ①和② B. ②和④ C. ②和③ D. ①和③

D 【解析】试题分析：①和③两个三角形有一个对应角相等，对应角的夹边也对应相等，所以①和③全等，故选D.