
科目: 来源:人教版九年级上册数学 24.2.2直线和圆的位置关系(2)练习 题型:单选题
若∠OAB=30°,OA=10cm,则以O为圆心,6cm为半径的圆与射线AB的位置关系是()
A. 相交 B. 相切 C. 相离 D. 不能确定
A 【解析】试题分析:圆心O到直线L的距离为d,圆的半径为r:当时,直线与圆相离;当时,直线与圆相切;当时,直线与圆相交. 由题意得点O到直线AB的距离为5 则以O为圆心,6cm为半径的圆与直线AB 的位置关系是相交 故选A.查看答案和解析>>
科目: 来源:人教版九年级上册数学 24.2.2直线和圆的位置关系(2)练习 题型:单选题
以三角形的一边长为直径的圆切三角形的另一边,则该三角形为()
A. 锐角三角形 B. 直角三角形 C. 钝角三角形 D. 等边三角形
B 【解析】根据切线的性质和三角形的特点可知,这个圆要过三角形的一边的两个顶点,又要与一边相切,则必有一边与圆只有一个交点,那么这边与作为直径的边就垂直,故三角形是直角三角形,故选B.查看答案和解析>>
科目: 来源:人教版九年级上册数学 24.2.2直线和圆的位置关系(2)练习 题型:单选题
如图,PA、PB分别切⊙O于A、B两点,C为劣弧AB上一点,∠APB=30°,则∠ACB=( )

A. 60° B. 75° C. 105° D. 120°
C 【解析】如图,连接AO,OB, 因为PA,PB分别切圆O于A,B两点, 所以∠PAO=∠PBO=90°, 所以∠AOB=180°-∠P=150°, 设点E是优弧AB上一点, 由圆周角定理可知, ∠E=75°, 由圆内接四边形的对角互补可知, ∠ACB=180°-∠E=105°, 故选C.查看答案和解析>>
科目: 来源:人教版九年级上册数学 24.2.2直线和圆的位置关系(2)练习 题型:单选题
已知△ABC的内切圆O与各边相切于D、E、F,那么点O是△DEF的()
A. 三条中线交点 B. 三条高的交点
C. 三条角平分线交点 D. 三条边的垂直平分线的交点
D 【解析】连接OE,OF,OD, 因为△ABC的内切圆O与各边分别相切于D,E,F三点, 所以OE⊥AB,OF⊥AC,OD⊥BC,OE=OF=OD, 即点O到△DEF的三个顶点的距离相等, 所以点O是△DEF的三条边的垂直平分线的交点, 故选D.查看答案和解析>>
科目: 来源:人教版九年级上册数学 24.2.2直线和圆的位置关系(2)练习 题型:解答题
如图AB,AC是⊙O的两条弦,∠A=30°,过点C的切线与OB的延长线交于点D,求∠D的度数.
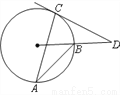
查看答案和解析>>
科目: 来源:人教版九年级上册数学 24.2.2直线和圆的位置关系(2)练习 题型:解答题
已知:如图,在RtΔABC中,∠C=90°,点0在AB上,以O为圆心,OA长为半径的圆与AC,AB分别交于点D,E,且∠CBD=∠A.判断直线BD与⊙O的位置关系,并证明你的结论.
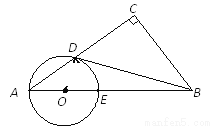
查看答案和解析>>
科目: 来源:人教版九年级上册数学 24.2.2直线和圆的位置关系(2)练习 题型:单选题
Rt△ABC中,∠C=90°,AB=10,AC=6,以C为圆心作⊙C和AB相切,则⊙C的半径长为()
A. 8 B. 4 C. 9.6 D. 4.8
D 【解析】作CD⊥AB于D,如图所示, 因为∠C=90°,AB=10,AC=6, 所以BC=8, 因为AC·BC=AB·CD, CD=, 因为⊙C与AB相切, 所以CD为⊙C的半径, 即的半径长为,故选D.查看答案和解析>>
科目: 来源:人教版九年级上册数学 24.2.2直线和圆的位置关系(2)练习 题型:单选题
从圆外一点向半径为9的圆作切线,已知切线长为18,从这点到圆的最短距离为( )
A. 9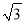 B. 9(
B. 9(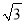 -1) C. 9(
-1) C. 9(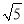 -1) D. 9
-1) D. 9
查看答案和解析>>
科目: 来源:人教版九年级上册数学 24.2.2直线和圆的位置关系(2)练习 题型:单选题
圆外一点P,PA、PB分别切⊙O于A、B,C为优弧AB上一点,若∠ACB=a,则∠APB=( )
A. 180°- 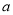 B. 90°-
B. 90°- 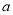 C. 90°+
C. 90°+ 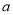 D. 180°-2
D. 180°-2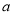
查看答案和解析>>
科目: 来源:人教版九年级上册数学 24.2.2直线和圆的位置关系(2)练习 题型:单选题
下列四边形中一定有内切圆的是()
A. 直角梯形 B. 等腰梯形 C. 矩形 D. 菱形
D 【解析】根据内切圆的定义即角平分线的交点到各边的距离相等,可知菱形一定有内切圆,故选D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com