
科目: 来源:北师大版(贵州)八年级数学下册:期末综合检测 题型:单选题
若x=3是分式方程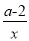 -
-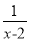 =0的根,则a的值是 ( )
=0的根,则a的值是 ( )
A. 5 B. -5 C. 3 D. -3
A 【解析】把x=3代入原分式方程得, ,解得,a=5,经检验a=5适合原方程. 故选A.查看答案和解析>>
科目: 来源:北师大版(贵州)八年级数学下册:期末综合检测 题型:单选题
已知等腰三角形的两边长分别是5和6,则这个等腰三角形的周长为( ).
A. 11 B. 16 C. 17 D. 16或17
D 【解析】试题分析:由等腰三角形的两边长分别是5和6,可以分情况讨论其边长为5,5,6或者5,6,6,均满足三角形两边之和大于第三边,两边之差小于第三边的条件,所以此等腰三角形的周长为5+5+6=16或5+6+6=17. 故选项D正确.查看答案和解析>>
科目: 来源:北师大版(贵州)八年级数学下册:期末综合检测 题型:单选题
遂宁市某生态示范园,计划种植一批核桃,原计划总产量达36万千克,为了满足市场需求,现决定改良核桃品种,改良后平均每亩产量是原计划的1.5倍,总产量比原计划增加了9万千克,种植亩数减少了20亩,则原计划和改良后平均每亩产量各是多少万千克?设原计划每亩平均产量为x万千克,则改良后平均每亩产量为1.5x万千克,根据题意列方程为( )
A. 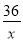 -
-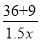 =20 B.
=20 B. 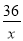 -
-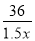 =20 C.
=20 C. 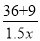 -
-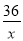 =20 D.
=20 D. 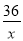 +
+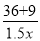 =20
=20
查看答案和解析>>
科目: 来源:北师大版(贵州)八年级数学下册:期末综合检测 题型:单选题
某电子元件厂准备生产4600个电子元件,甲车间独立生产了一半后,由于要尽快投入市场,乙车间也加入该电子元件的生产,若乙车间每天生产的电子元件是甲车间的1.3倍,结果用33天完成任务,则甲车间每天生产电子元件多少个?在这个问题中设甲车间每天生产电子元件x个,根据题意可得方程为 ( )
A. 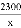 +
+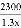 =33
=33
B. 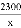 +
+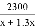 =33
=33
C. 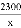 +
+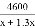 =33
=33
D. 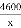 +
+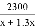 =33
=33
查看答案和解析>>
科目: 来源:北师大版(贵州)八年级数学下册:期末综合检测 题型:单选题
如图所示,四边形ABCD中,对角线AC,BD相交于点O,下列条件不能判定这个四边形是平行四边形的是 ( )
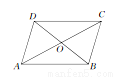
A. AB∥DC,AD∥BC
B. AB=DC,AD=BC
C. AO=CO,BO=DO
D. AB∥DC,AD=BC
D 【解析】试题分析:A、根据两组对边分别平行的四边形为平行四边形;B、根据两组对边分别相等的四边形为平行四边形;C、根据对角线互相平分的四边形是平行四边形;D、不能判定.查看答案和解析>>
科目: 来源:北师大版(贵州)八年级数学下册:期末综合检测 题型:单选题
把代数式3x3-12x2+12x分解因式,结果正确的是 ( )
A. 3x(x2-4x+4) B. 3x(x-4)2
C. 3x(x+2)(x-2) D. 3x(x-2)2
D 【解析】3x3-12x2+12x=3x(x2-4x+4)=3x(x-2)2 故选D.查看答案和解析>>
科目: 来源:北师大版(贵州)八年级数学下册:期末综合检测 题型:单选题
平行四边形ABCD中,E,F是对角线BD上的两点, 如果添加一个条件使△ABE≌△CDF,则添加的条件不能是( )
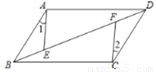
A. AE=CF B. BE=FD C. BF=DE D. ∠1=∠2
C 【解析】试题分析:因为四边形ABCD是平行四边形,所以AB//CD,AB=CD,所以∠ABD=∠CDB,所以要使△ABE≌△CDF, 若添加条件:∠1=∠2,可以利用ASA证明△ABE≌△CDF,所以D正确,若添加条件:BE=FD,可以利用SAS证明△ABE≌△CDF,所以B正确,若添加条件:BF=DE,可以得到BE=FD,可以利用SAS证明△ABE≌△CDF,所以C正确;若添加条...查看答案和解析>>
科目: 来源:北师大版(贵州)八年级数学下册:期末综合检测 题型:填空题
如图所示,在Rt△ABC中,∠C=90°,AC=4,将△ABC沿CB向右平移得到△DEF,若平移距离为2,则四边形ABED的面积等于 .
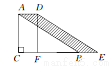
查看答案和解析>>
科目: 来源:北师大版(贵州)八年级数学下册:期末综合检测 题型:填空题
如图所示,在△ABC中,∠C=90°,∠CAB=50°.按以下步骤作图:①以点A为圆心,小于AC的长为半径画弧,分别交AB,AC于点E,F;②分别以点E,F为圆心,大于 EF的长为半径画弧,两弧相交于点G;③作射线AG交BC边于点D.则∠ADC的度数为 .
EF的长为半径画弧,两弧相交于点G;③作射线AG交BC边于点D.则∠ADC的度数为 .
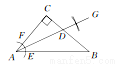
查看答案和解析>>
科目: 来源:北师大版(贵州)八年级数学下册:期末综合检测 题型:填空题
分式方程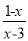 =
=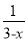 -2的解为 .
-2的解为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com