
科目: 来源:天津市宝坻区口东镇2017-2018学年八年级12月月考数学试卷 题型:解答题
对于分式 ,当x=___时,分式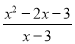 无意义;当x=_________时,分式值为零.
无意义;当x=_________时,分式值为零.
【答案】 3 -1
【解析】分母等于0,分式无意义,由此可得x-3=0,即x=3,所以当x=3时,分式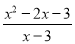 无意义;
无意义;
分式的值为零,分子为0,分母不为0,由此可得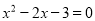 且x≠3,解得x=-1,所以当x=-1时,分式
且x≠3,解得x=-1,所以当x=-1时,分式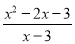 的值为零.
的值为零.
点睛:本题考查了分式无意义及分式的值为0的条件:①分母等于0,分式无意义;②分式的值为零,分子为0,分母不为0.
【题型】填空题
【结束】
20
已知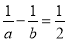 ,则
,则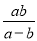 的值是_____________.
的值是_____________.
查看答案和解析>>
科目: 来源:天津市宝坻区口东镇2017-2018学年八年级12月月考数学试卷 题型:解答题
已知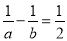 ,则
,则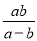 的值是_____________.
的值是_____________.
【答案】-2
【解析】试题解析:∵ 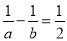
∴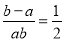
∴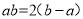
∴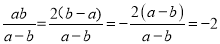
【题型】解答题
【结束】
21
计算下列各题:
(1)(﹣2a)6﹣(﹣3a3)2+[﹣(2a)2]3
(2)(16x4﹣8x3+4x2)÷(﹣2x)2
(3)(2x﹣y)2﹣4(x﹣y)(x+2y)
(1)﹣9a6;(2) 4x2﹣2x+1;(3)﹣8xy+9y2. 【解析】试题分析:(1)利用积的乘方与幂的乘方运算法则计算后,合并即可得到结果; (2)利用多项式除以单项式的运算法则计算即可;(3)先利用乘法公式及多项式乘以多项式的运算法则计算后,再合并即可得结果. 试题解析: (1)原式=64a6﹣9a6﹣64a6=﹣9a6; (2)原式=(16x4﹣8x3+4x2)...查看答案和解析>>
科目: 来源:天津市宝坻区口东镇2017-2018学年八年级12月月考数学试卷 题型:解答题
计算下列各题:
(1)(﹣2a)6﹣(﹣3a3)2+[﹣(2a)2]3
(2)(16x4﹣8x3+4x2)÷(﹣2x)2
(3)(2x﹣y)2﹣4(x﹣y)(x+2y)
【答案】(1)﹣9a6;(2) 4x2﹣2x+1;(3)﹣8xy+9y2.
【解析】试题分析:(1)利用积的乘方与幂的乘方运算法则计算后,合并即可得到结果; (2)利用多项式除以单项式的运算法则计算即可;(3)先利用乘法公式及多项式乘以多项式的运算法则计算后,再合并即可得结果.
试题解析:
(1)原式=64a6﹣9a6﹣64a6=﹣9a6;
(2)原式=(16x4﹣8x3+4x2)÷4x2=4x2﹣2x+1;
(3)原式=4x2﹣4xy+y2﹣4(x2﹣2xy﹣xy﹣2y2)=4x2﹣4xy+y2﹣4x2+8xy+4xy+8y2=﹣8xy+9y2.
【题型】解答题
【结束】
22
对下列多项进行因式分【解析】
(1).(x+2)(x+4)+1.
(2).x2﹣5x﹣6
(3).(a2+4)2﹣16a2
(4).18b(a﹣b)2﹣12(a﹣b)3
(1)(x+3)2(2)(x﹣6)(x+1);(3)(a+2)2(a﹣2)2;(4) 6(a﹣b)2(5b﹣2a) 【解析】试题分析:(1)先展开合并后利用完全平方公式因式分解即可;(2)利用十字相乘法因式分解即可;(3)先利用平方差公式,再利用完全平方公式分解因式即可;(4)直接利用提公因式法因式分解即可. 试题解析: (1)原式=x2+6x+9=(x+3)2. (2)原...查看答案和解析>>
科目: 来源:天津市宝坻区口东镇2017-2018学年八年级12月月考数学试卷 题型:解答题
对下列多项进行因式分【解析】
(1).(x+2)(x+4)+1.
(2).x2﹣5x﹣6
(3).(a2+4)2﹣16a2
(4).18b(a﹣b)2﹣12(a﹣b)3
【答案】(1)(x+3)2(2)(x﹣6)(x+1);(3)(a+2)2(a﹣2)2;(4) 6(a﹣b)2(5b﹣2a)
【解析】试题分析:(1)先展开合并后利用完全平方公式因式分解即可;(2)利用十字相乘法因式分解即可;(3)先利用平方差公式,再利用完全平方公式分解因式即可;(4)直接利用提公因式法因式分解即可.
试题解析:
(1)原式=x2+6x+9=(x+3)2.
(2)原式=(x﹣6)(x+1);
(3)原式=(a2+4+4a)(a2+4﹣4a)=(a+2)2(a﹣2)2;
(4)原式=6(a﹣b)2(3b﹣2a+2b)=6(a﹣b)2(5b﹣2a);
【题型】解答题
【结束】
23
计算下列各分式:
(1). 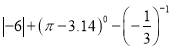
(2). 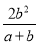 -a+b
-a+b
(3). 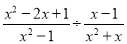
查看答案和解析>>
科目: 来源:天津市宝坻区口东镇2017-2018学年八年级12月月考数学试卷 题型:解答题
计算下列各分式:
(1). 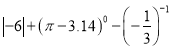
(2). 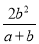 -a+b
-a+b
(3). 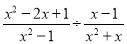
【答案】(1)10(2) 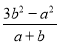 (3)x
(3)x
【解析】试题分析:(1)根据绝对值的性质、零指数幂、负整数指数幂分别计算各项后,合并即可;(2)通分后化简即可;(3)把除法转化为乘法后约分即可.
试题解析:
(1)原式=6+1+3=10.
(2)原式=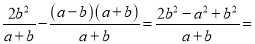
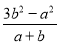 ;
;
(3)原式=  .
.
【题型】解答题
【结束】
24
先化简,再求代数式的值: 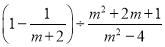 ,其中m=1.
,其中m=1.
查看答案和解析>>
科目: 来源:天津市宝坻区口东镇2017-2018学年八年级12月月考数学试卷 题型:解答题
先化简,再求代数式的值: 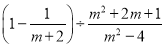 ,其中m=1.
,其中m=1.
【答案】(1) 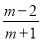 ,
, 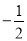
【解析】先进行分式的混合运算,再代入求值即可.
【解析】
原式= ,
,
= ,
,
=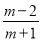 ;
;
当m =1时,原式=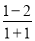 =-
=-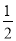 .
.
【题型】解答题
【结束】
25
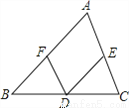
如图,在△ABC中,D为BC边的中点,过D点分别作DE∥AB交AC于点E,DF∥AC交AB于点F.
求证:BF=DE.
查看答案和解析>>
科目: 来源:天津市宝坻区口东镇2017-2018学年八年级12月月考数学试卷 题型:解答题
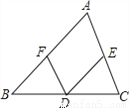
如图,在△ABC中,D为BC边的中点,过D点分别作DE∥AB交AC于点E,DF∥AC交AB于点F.
求证:BF=DE.
【答案】证明见解析
【解析】试题分析:根据两组对边分别平行的四边形为平行四边形可判定四边形AFDE是平行四边形,根据平行四边形的性质可得DE=AF,再由D为BC边的中点,DF∥AC,可得BF=AF,即可得BF=DE.
试题解析:
∵DE∥AB,DF∥AC,
∴DE∥AF,DF∥AE,
∴四边形AFDE是平行四边形,
∴DE=AF,
∵D为BC边的中点,
∴BD=DC,∵DF∥AC,
∴BF=AF,
∴BF=DE.
【题型】解答题
【结束】
26
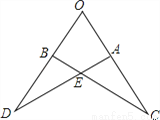
如图,已知:∠C=∠D,OD=OC.求证:DE=CE.
查看答案和解析>>
科目: 来源:天津市宝坻区口东镇2017-2018学年八年级12月月考数学试卷 题型:解答题
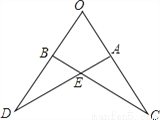
如图,已知:∠C=∠D,OD=OC.求证:DE=CE.
【答案】证明见解析
【解析】试题分析:利用ASA证明△OBC≌△OAD,根据全等三角形的对应边相等可得OA=OB,再由OD=OC,即可得AC=BD,根据AAS证明△ACE≌△BDE,再由全等三角形的对应边相等即可得结论.
试题解析:
在△OBC和△OAD中,
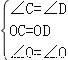 ,
,
∴△OBC≌△OAD(ASA),
∴OA=OB,
∵OD=OC,
∴OD﹣OB=OC﹣OA,即AC=BD,
在△ACE和△BDE中,
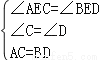 ,
,
∴△ACE≌△BDE(AAS),
∴DE=CE.
【题型】解答题
【结束】
27
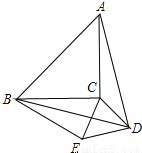
如图,以等腰直角三角形ABC的斜边AB为边向内作等边△ABD,连接DC,以DC为边,作等边△DCE,点B、E在CD的同侧.
(1)求∠BCE的大小;
(2)求证:BE=AC.
查看答案和解析>>
科目: 来源:山东省临沂市2018届九年级(上)第一次月考数学试卷 题型:单选题
下列方程是关于x的一元二次方程的是( )
A. x2+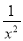 =0 B. ax2+bx+c=0 C. (x+1)(x﹣2)=1 D. 3x2﹣2xy﹣5y2=0
=0 B. ax2+bx+c=0 C. (x+1)(x﹣2)=1 D. 3x2﹣2xy﹣5y2=0
查看答案和解析>>
科目: 来源:山东省临沂市2018届九年级(上)第一次月考数学试卷 题型:单选题
用配方法解方程x2-2x-1=0时,配方后得的方程为( )
A. (x+1)2=0 B. (x-1)2=0 C. (x+1)2=2 D. (x-1)2=2
D 【解析】试题分析:把方程x2-2x-1=0的常数项移到等号的右边,得到x2-2x=1, 方程两边同时加上一次项系数一半的平方,得到x2-2x+1=1+1 配方得(x-1)2=2. 故选D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com