
科目: 来源:安徽省芜湖市教育集团2017-2018学年度上学期八年级第二次月考 题型:解答题
计算:
(1)、(x+y)2﹣(x+y)(x﹣y) (2)、(3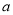 +2b﹣1)(3
+2b﹣1)(3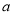 ﹣2b+1)
﹣2b+1)
查看答案和解析>>
科目: 来源:安徽省芜湖市教育集团2017-2018学年度上学期八年级第二次月考 题型:解答题
对下列多项式进行因式分【解析】
(1)、9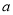 2(x﹣y)+4b2(y﹣x). (2)、4
2(x﹣y)+4b2(y﹣x). (2)、4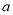 (1-b)2+2(b-1)2
(1-b)2+2(b-1)2
查看答案和解析>>
科目: 来源:安徽省芜湖市教育集团2017-2018学年度上学期八年级第二次月考 题型:解答题
如图,BD=CD,∠B=∠C,求证:AD平分∠BAC。
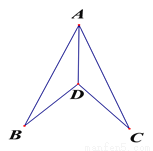
查看答案和解析>>
科目: 来源:安徽省芜湖市教育集团2017-2018学年度上学期八年级第二次月考 题型:解答题
阅读下列解答过程,然后回答问题.已知多项式x3+4x2+mx+5有一个因式(x+1),求m的值.
【解析】
设另一个因式为(x2+ax+b),
则x3+4x2+mx+5=(x+1)(x2+ax+b)=x2+(a+1)x2+(a+b)x+b,
∴a+1=4,a+b=m,b=5,∴a=3,b=5,∴m=8;
依照上面的解法,解答问题:若x3+3x2﹣3x+k有一个因式是x+1,求k的值.
-5. 【解析】试题分析:将一个多项式化成几个单项式或单项式乘积的形式时,如果有一个因式为零时,则整个多项式的值为零.本题中假设x+1=0求出x的值,从而将x的值代入代数式求出k的值. 试题解析:∵多项式x3+4x2+mx+5有一个因式(x+1), ∴令x+1=0得x=﹣1,即当x=﹣1时,原多项式为零, ∴(﹣1)3+3×(﹣1)2﹣3×(﹣1)+k=0, ∴k=﹣...查看答案和解析>>
科目: 来源:安徽省芜湖市教育集团2017-2018学年度上学期八年级第二次月考 题型:解答题
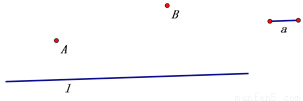
已知A、B两点在直线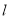 的同侧,试在
的同侧,试在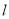 上找两点C和D(CD的长度为定值
上找两点C和D(CD的长度为定值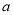 ),使得AC+CD+DB最短(保留作图痕迹,不要求写画法)。
),使得AC+CD+DB最短(保留作图痕迹,不要求写画法)。
查看答案和解析>>
科目: 来源:安徽省芜湖市教育集团2017-2018学年度上学期八年级第二次月考 题型:解答题
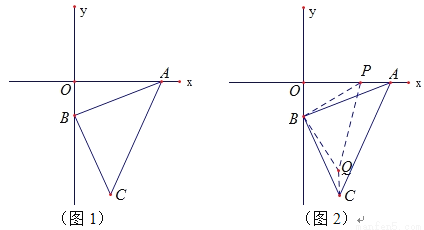
如图,已知A(3,0),B(0,-1),连接AB,过B点作AB的垂线段,使BA=BC,连接AC.
(1)如图1,求C点坐标;
(2)如图2,若P点从A点出发,沿x轴向左平移,连接BP,作等腰直角三角形△BPQ,连接CQ.求证:PA=CQ.
(3)在(2)的条件下,若C、P、Q三点共线,求此时P点坐标及∠APB的度数.
查看答案和解析>>
科目: 来源:黄金30题系列 九年级数学 小题好拿分 题型:单选题
如图,BD是⊙O的直径,点A、C在⊙O上,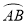 =
=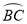 ,∠AOB=60°,则∠BDC的度数是( ).
,∠AOB=60°,则∠BDC的度数是( ).
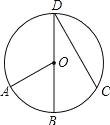
A.60° B.45° C.35° D.30°
D. 【解析】 试题分析:直接根据圆周角定理求解.连结OC,如图,∵=,∴∠BDC=∠BOC=∠AOB=×60°=30°. 故选:D.查看答案和解析>>
科目: 来源:黄金30题系列 九年级数学 小题好拿分 题型:单选题
已知二次函数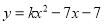 的图象和x轴有交点,则k的取值范围是 ( )
的图象和x轴有交点,则k的取值范围是 ( )
A. k>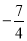 B. k≥
B. k≥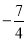 C. k≥
C. k≥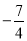 且k≠0 D. k>
且k≠0 D. k>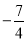 且k≠0
且k≠0
查看答案和解析>>
科目: 来源:黄金30题系列 九年级数学 小题好拿分 题型:单选题
边长分别等于6 cm、8 cm、10cm的三角形的内切圆的半径为( )cm.
A. 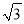 B.
B. 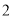 C.
C. 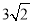 D.
D. 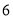
查看答案和解析>>
科目: 来源:黄金30题系列 九年级数学 小题好拿分 题型:单选题
如图,市政府准备修建一座高AB=6m的过街天桥,已知天桥的坡面AC与地面BC的夹角∠ACB的正弦值为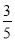 ,则坡面AC的长度为( )m.
,则坡面AC的长度为( )m.
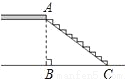
A.10 B.8 C.6 D.6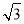
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com