
科目: 来源:甘肃省武威市2017-2018学年八年级(上)期中数学试卷 题型:填空题
在下列条件中:①∠A+∠B=∠C,②∠A:∠B:∠C=1:2:3,③∠A=90°﹣∠B,④∠A=∠B=∠C中,能确定△ABC是直角三角形的条件有_____(填序号)
①②③ 【解析】∵∠A+∠B=∠C, ∠A+∠B+∠C=180°,∴2∠C=180°,∠C=90°,∴△ABC是直角三角形; ∵∠A:∠B:∠C=1:2:3,设∠A=x,则x+2x+3x=180,x=30°,∠C=30°×3=90°,∴△ABC是直角三角形; ∵∠A=90°?∠B,∴∠A+∠B=90°,则∠C=180°?90°=90°,∴△ABC是直角三角形; ∵∠A=∠B...查看答案和解析>>
科目: 来源:甘肃省武威市2017-2018学年八年级(上)期中数学试卷 题型:填空题
如图,等腰三角形ABC底边BC的长为4cm,面积是12cm2,腰AB的垂直平分线EF交AC于点F,若D为BC边上的中点,M为线段EF上一动点,则△BDM的周长最短为_____cm.
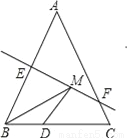
查看答案和解析>>
科目: 来源:甘肃省武威市2017-2018学年八年级(上)期中数学试卷 题型:解答题
在图中求作一点P,使点P到∠AOB两边的距离相等,并且使OP等于MN,不写作法,保留作图痕迹.(要求:用尺规作图)
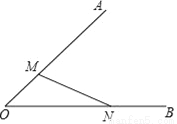
查看答案和解析>>
科目: 来源:甘肃省武威市2017-2018学年八年级(上)期中数学试卷 题型:解答题
已知AB∥DE,BC∥EF,D,C在AF上,且AD=CF,求证:△ABC≌△DEF.
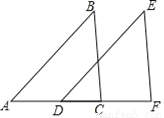
查看答案和解析>>
科目: 来源:甘肃省武威市2017-2018学年八年级(上)期中数学试卷 题型:解答题
如图,点D、E在△ABC的BC边上,AB=AC,AD=AE.求证:BD=CE.
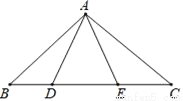
查看答案和解析>>
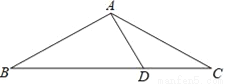
科目: 来源:甘肃省武威市2017-2018学年八年级(上)期中数学试卷 题型:解答题
如图,在△ABC中,AB=AC,∠C=30°,AB⊥AD,AD=4cm,求BC的长.
查看答案和解析>>
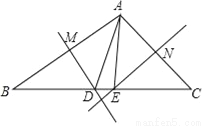
科目: 来源:甘肃省武威市2017-2018学年八年级(上)期中数学试卷 题型:解答题
如图,在△ABC中,BC=8,AB的中垂线交BC于D,AC的中垂线交BC于E,求△ADE的周长.
查看答案和解析>>
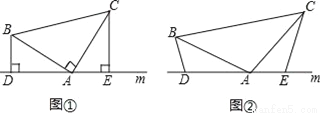
科目: 来源:甘肃省武威市2017-2018学年八年级(上)期中数学试卷 题型:解答题
(1)已知,如图①,在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E,求证:DE=BD+CE.
(2)如图②,将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意钝角,请问结论DE=BD+CE是否成立?若成立,请你给出证明:若不成立,请说明理由.
查看答案和解析>>
科目: 来源:黄金30题系列 九年级数学 小题易丢分 题型:单选题
下列图形中,既是轴对称图形又是中心对称图形的是( )
A.  B.
B. 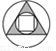 C.
C.  D.
D. 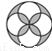
查看答案和解析>>
科目: 来源:黄金30题系列 九年级数学 小题易丢分 题型:单选题
如图,已知一块圆心角为270°的扇形铁皮,用它作一个圆锥形的烟囱帽(接缝忽略不计),圆锥底面圆的直径是60cm,则这块扇形铁皮的半径是( )
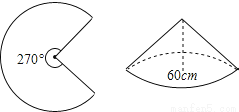
A. 40cm B. 50cm C. 60cm D. 80cm
A 【解析】试题解析:∵圆锥的底面直径为60cm, ∴圆锥的底面周长为60πcm, ∴扇形的弧长为60πcm 设扇形的半径为r,则, 解得:r=40cm, 故选A.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com