
科目: 来源:山东省2018届九年级12月月考数学试卷 题型:填空题
如图:某同学用一个有60°角的直角三角板估测学校旗杆AB的高度,他将60°角的直角边水平放在1.5米高的支架CD上,三角板的斜边与旗杆的顶点在同一直线上,他又量得D、B的距离为5米,则旗杆AB的高度约为__________米。
10.2米 【解析】在△ACE中,CE⊥AE,tan∠ACE=,由此可以求出AE.再根据AB=AE+BE=AE+CD即可求解. 【解析】 由题意可知, 在△ACE中,CE⊥AE,且∠ACE=60°,BD=5, 而tan∠ACE=, ∴AE=CE×tan60°=5. 又∵EB=1.5, ∴AB=AE+EB=AE+CD=+1.5≈10.2(米).查看答案和解析>>
科目: 来源:山东省2018届九年级12月月考数学试卷 题型:解答题
解方程:
(1)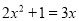 (配方法)
(配方法)
(2)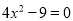 (因式分解法)
(因式分解法)
(3)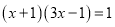 ( 公式法)
( 公式法)
查看答案和解析>>
科目: 来源:山东省2018届九年级12月月考数学试卷 题型:解答题
如图,点D,E在BC上,且FD∥AB,FE∥AC.求证:△ABC∽△FDE.
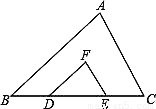
查看答案和解析>>
科目: 来源:山东省2018届九年级12月月考数学试卷 题型:解答题
若方程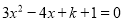 无实数根,化简:
无实数根,化简: 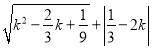
查看答案和解析>>
科目: 来源:山东省2018届九年级12月月考数学试卷 题型:解答题
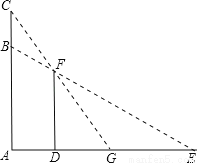
如图,一只猫头鹰蹲在一棵树AC的B(点B在AC上)处,发现一只老鼠躲进短墙DF的另一侧,猫头鹰的视线被短墙遮住,为了寻找这只老鼠,它又飞至树顶C处,已知短墙高DF=4米,短墙底部D与树的底部A的距离为2.7米,猫头鹰从C点观测F点的俯角为53°,老鼠躲藏处M(点M在DE上)距D点3米.
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
(1)猫头鹰飞至C处后,能否看到这只老鼠?为什么?
(2)要捕捉到这只老鼠,猫头鹰至少要飞多少米(精确到0.1米)?
查看答案和解析>>
科目: 来源:山东省2018届九年级12月月考数学试卷 题型:解答题
某电视机厂计划用两年的时间把某种型号的电视机的成本降低36%, 若每年下降的百分数相同,求这个百分数.
20% 【解析】本题主要考查了一元二次方程的应用. 可设原来的成本为1.等量关系为:原来的成本×(1-每年下降的百分数)2=原来的成本×(1-36%),把相关数值代入求合适解即可. 【解析】 设每年下降的百分数为x. 1×(1-x)2=1×(1-36%), ∵1-x>0, ∴1-x=0.8, ∴x=20%.查看答案和解析>>
科目: 来源:山东省2018届九年级12月月考数学试卷 题型:解答题
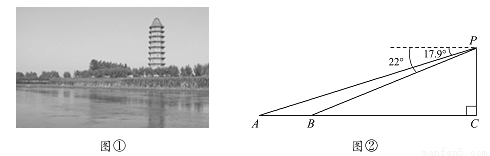
如图,耸立在临清市城北大运河东岸的舍利宝塔,是“运河四大名塔”之一(如图①),数学兴趣小组的小亮同学在塔上观景点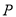 处,利用测角仪测得运河两岸上的
处,利用测角仪测得运河两岸上的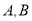 两点的俯角分别为
两点的俯角分别为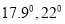 ,并测得塔底点
,并测得塔底点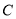 到点
到点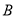 的距离为
的距离为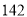 米(
米(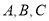 在同一直线上,如图②)求运河两岸的
在同一直线上,如图②)求运河两岸的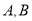 两点的距离(精确到1米)
两点的距离(精确到1米)
(参考数据: 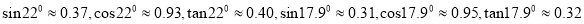 )
)
查看答案和解析>>
科目: 来源:山东省2018届九年级12月月考数学试卷 题型:解答题
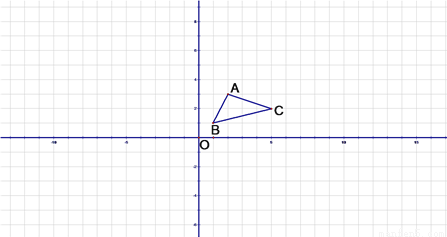
如图,A(2,3),B(1,1),C(5,2)以原点O为位似中心,相似比为2, 将△ABC进行变换,画出变换后的图形,并求出相应的坐标.
查看答案和解析>>
科目: 来源:山东省2018届九年级12月月考数学试卷 题型:解答题
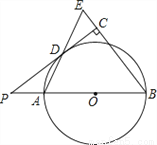
如图,已知AB是⊙O的直径,点P在BA的延长线上,PD切⊙O于点D,过点B作BE垂直于PD,交PD的延长线于点C,连接AD并延长,交BE于点E.
(1)求证:AB=BE;
(2)若PA=2,cosB=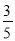 ,求⊙O半径的长.
,求⊙O半径的长.
查看答案和解析>>
科目: 来源:2017年吉林省长春市中考数学模拟试卷(7) 题型:单选题
比﹣1小2的数是( )
A. ﹣3 B. ﹣2 C. ﹣1 D. 3
A 【解析】比?1小2的数是就是?1与2的差,即?1?2=?3. 故选:A.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com