
科目: 来源:2017年山东省临沂市中考数学二模试卷(一) 题型:解答题
初二年级教师对试卷讲评课中学生参与的深度与广度进行评价调查,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项.评价组随机抽取了若干名初二学生的参与情况,绘制成如图所示的频数分布直方图和扇形统计图(均不完整),请根据图中所给信息解答下列问题:
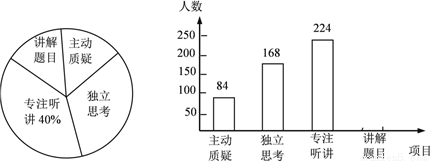
(1)在这次评价中,一共抽查了 名学生;
(2)在扇形统计图中,项目“主动质疑”所在的扇形的圆心角的度数为 度;
(3)请将频数分布直方图补充完整;
(4)如果全市有6000名初二学生,那么在试卷评讲课中,“独立思考”的初二学生约有多少人?
(1)560;(2)54 ;(3)见解析;(4)1800 【解析】试题分析:(1)、根据专注听讲的人数是224人,所占的比例是40%,即可求得抽查的总人数;(2)、利用360乘以对应的百分比即可求解;(3)、利用总人数减去其他各组的人数,即可求得讲解题目的人数,从而作出频数分布直方图;(4)、利用6000乘以对应的比例即可. 试题解析:(1)、调查的总人数是:224÷40%=560(人...查看答案和解析>>
科目: 来源:2017年山东省临沂市中考数学二模试卷(一) 题型:解答题
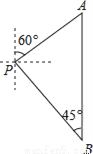
如图,小明从P点出发,沿北偏东60°方向行驶到达A处,接着向正南方向行驶100(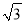 +1)米到达B处.在B处观测到出发时所在的P处在北偏西45°方向上,P,A两处相距多少米?
+1)米到达B处.在B处观测到出发时所在的P处在北偏西45°方向上,P,A两处相距多少米?
查看答案和解析>>
科目: 来源:2017年山东省临沂市中考数学二模试卷(一) 题型:解答题
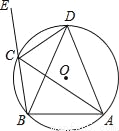
如图,已知点A,B,C,D均在⊙O上,CD为∠ACE的角平分线.
(1)求证:△ABD为等腰三角形;
(2)若∠DCE=45°,BD=6,求⊙O的半径.
查看答案和解析>>
科目: 来源:2017年山东省临沂市中考数学二模试卷(一) 题型:解答题
开发区某企业生产的产品每件出厂价为50元,成本价为25元,在生产过程中,平均每生产一件产品有0.5m3污水排出,为了绿色环保达到排污标准,工厂设计两种处理污水的方案,
方案一:工厂污水先净化处理后再排出,每处理1m3污水的费用为2元,并且每月排污设备损耗为30000元.
方案二:工厂将污水排到污水厂统一处理,每处理1m3污水的费用为14元.
设工厂每月生产x件产品,每月利润为y元,
(1)分别写出依据方案一和方案二处理污水时,y与x的关系式;
(2)如果你是该企业的负责人,如何根据企业的生产实际选择污水处理方案?
(1)方案一:y1=24x﹣30000;方案二:y2=18x;(2)当工厂每月生产5000件产品时,两种方案利润相同,当超过5000件时,方案一利润大,当低于5000件时,方案二利润大 【解析】试题分析:(1)每件产品出厂价为50元,共x件,则总收入为:50x,成本费为25x,产生的污水总量为0.5x,按方案一处理污水应花费:2x×0.5+30000,按方案二处理应花费:25x+0.5x×1...查看答案和解析>>
科目: 来源:2017年山东省临沂市中考数学二模试卷(一) 题型:解答题
【发现证明】
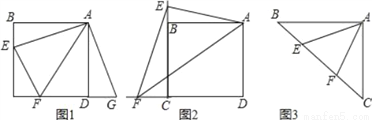
如图1,点E,F分别在正方形ABCD的边BC,CD上,∠EAF=45°,试判断BE,EF,FD之间的数量关系.
小聪把△ABE绕点A逆时针旋转90°至△ADG,通过证明△AEF≌△AGF;从而发现并证明了EF=BE+FD.
【类比引申】
(1)如图2,点E、F分别在正方形ABCD的边CB、CD的延长线上,∠EAF=45°,连接EF,请根据小聪的发现给你的启示写出EF、BE、DF之间的数量关系,并证明;
【联想拓展】
(2)如图3,如图,∠BAC=90°,AB=AC,点E、F在边BC上,且∠EAF=45°,若BE=3,EF=5,求CF的长.
查看答案和解析>>
科目: 来源:2017年山东省临沂市中考数学二模试卷(一) 题型:解答题
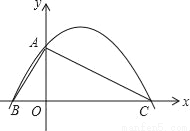
如图,在平面直角坐标系中,△ABC的边BC在x轴上,顶点A在y轴的正半轴上,OA=2,OB=1,OC=4.
(1)求过A、B、C三点的抛物线的解析式;
(2)设点M是x轴上的动点,试问:在平面直角坐标系中,是否存在点N,使得以点A,B,M,N为顶点的四边形是菱形?若存在,直接写出点N的坐标;若不存在,说明理由;
(3)若抛物线对称轴交x轴于点P,在平面直角坐标系中,是否存在点Q,使△PAQ是以PA为腰的等腰直角三角形?若存在,写出所有符合条件的点Q的坐标,选择一种情况加以说明;若不存在,说明理由.
查看答案和解析>>
科目: 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷(八) 题型:单选题
连接海口、文昌两市的跨海大桥﹣﹣铺前大桥,近日获国家发改委批准建设,该桥估计总投资约为1460000000元,数据1460000000用科学记数法表示应是( )
A. 1.46×107 B. 1.46×109 C. 1.46×1010 D. 0.146×1010
B 【解析】根据科学记数法的定义,科学记数法的表示形式为a×10n,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值。在确定n的值时,看该数是大于或等于1还是小于1。当该数大于或等于1时,n为它的整数位数减1;当该数小于1时,-n为它第一个有效数字前0的个数(含小数点前的1个0)。1 460 000 000一共10位,从而1 460 000 000=1.46×109。故选...查看答案和解析>>
科目: 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷(八) 题型:单选题
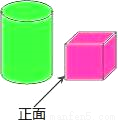
如图,小明从正面观察一个圆柱体邮筒和一个正方体箱子,看到的是( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目: 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷(八) 题型:单选题
下列运算正确的是( )
A. (﹣2x2)3=﹣6x6 B. x4÷x2=x2
C. 2x+2y=4xy D. (x+y)(﹣y+x)=y2﹣x2
B 【解析】分析:根据积的乘方,先把每一个因式分别乘方,再把所得的幂相乘;同底数幂相除,底数不变指数相减;平方差公式,对各选项分析判断后利用排除法. 解答:【解析】 A、应为(-2x2)3=-8x6,故本选项错误; B、x4÷x2=x4-2=x2,正确; C、2x+2y是相加,不是相乘,所以计算错误,故本选项错误; D、应为(x+y)(-y+x)=x2-y2,故本选...查看答案和解析>>
科目: 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷(八) 题型:单选题
一个盒子内装有大小、形状相同的四个球,其中红球1个、绿球1个、白球2个,小明摸出一个球不放回,再摸出一个球,则两次都摸到白球的概率是( )
A. 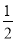 B.
B. 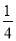 C.
C. 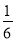 D.
D. 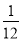
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com