
科目: 来源:浙江省杭州市2018届九年级上学期期中考试数学试卷(含解析) 题型:填空题
抛物线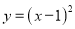 的顶点坐标是__________.
的顶点坐标是__________.
查看答案和解析>>
科目: 来源:浙江省杭州市2018届九年级上学期期中考试数学试卷(含解析) 题型:填空题
从长度为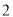 ,
, 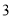 ,
, 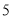 ,
, 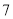 的四条线段中任意选取三条,能构成三角形的概率为__________.
的四条线段中任意选取三条,能构成三角形的概率为__________.
查看答案和解析>>
科目: 来源:浙江省杭州市2018届九年级上学期期中考试数学试卷(含解析) 题型:填空题
如图所示,已知⊙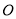 是
是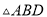 的外接圆,
的外接圆, 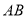 是⊙
是⊙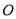 的直径,
的直径, 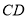 是⊙
是⊙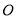 的弦,
的弦, 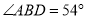 ,则
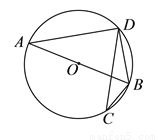
,则 __________.
__________.
查看答案和解析>>
科目: 来源:浙江省杭州市2018届九年级上学期期中考试数学试卷(含解析) 题型:填空题
把二次函数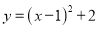 的图象绕原点旋转
的图象绕原点旋转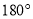 后得的图象的解析式为__________.
后得的图象的解析式为__________.
查看答案和解析>>
科目: 来源:浙江省杭州市2018届九年级上学期期中考试数学试卷(含解析) 题型:填空题
如图,已知线段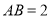 ,
, 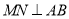 于点
于点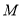 ,且
,且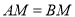 ,
, 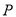 是射线
是射线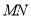 上一动点,
上一动点, 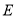 、
、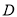 分别是
分别是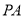 ,
, 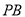 的中点,过点
的中点,过点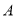 ,
, 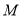 ,
, 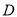 的圆与
的圆与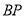 的另一交点
的另一交点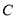 (点
(点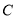 在线段
在线段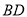 上),连结
上),连结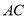 ,
, 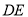 .
.
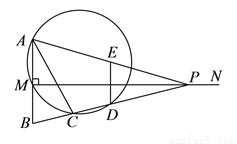
( )当
)当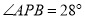 时,则
时,则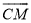 的度数为__________.
的度数为__________.
( )在点
)在点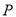 的运动过程中,当
的运动过程中,当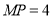 时,取四边形
时,取四边形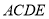 一边的两端点和线段
一边的两端点和线段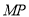 上一点
上一点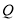 ,若以这三点为顶点的三角形是直角三角形,当
,若以这三点为顶点的三角形是直角三角形,当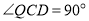 时,则
时,则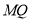 的值为__________.
的值为__________.
查看答案和解析>>
科目: 来源:浙江省杭州市2018届九年级上学期期中考试数学试卷(含解析) 题型:填空题
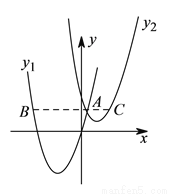
如图,将二次函数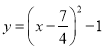 的图像向上平移
的图像向上平移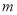 个单位得到二次函数
个单位得到二次函数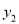 的图像,且与二次函数
的图像,且与二次函数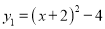 的图像相交于
的图像相交于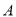 ,过
,过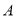 作
作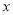 轴的平行线分别交
轴的平行线分别交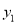 ,
, 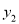 于点
于点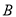 ,
, 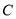 ,当
,当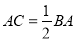 时,
时, 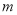 的值是__________.
的值是__________.
查看答案和解析>>
科目: 来源:浙江省杭州市2018届九年级上学期期中考试数学试卷(含解析) 题型:解答题
如图:电路图上有四个开关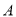 、
、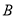 、
、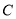 、
、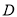 和一个小灯泡,闭合开关
和一个小灯泡,闭合开关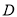 或同时闭合开关
或同时闭合开关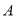 ,
, 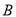 ,
, 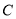 都可使小灯泡发光.
都可使小灯泡发光.
( )任意闭合其中一个开关,则小灯泡发光的概率等于__________.
)任意闭合其中一个开关,则小灯泡发光的概率等于__________.
( )任意闭合其中两个开关,请画树状图或列表的方法求出小灯泡发光的概率.
)任意闭合其中两个开关,请画树状图或列表的方法求出小灯泡发光的概率.
查看答案和解析>>
科目: 来源:浙江省杭州市2018届九年级上学期期中考试数学试卷(含解析) 题型:解答题
若函数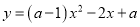 的图象与坐标轴有两个交点,求
的图象与坐标轴有两个交点,求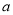 的值.
的值.
查看答案和解析>>
科目: 来源:浙江省杭州市2018届九年级上学期期中考试数学试卷(含解析) 题型:解答题
已知:如图, 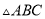 内接于⊙
内接于⊙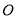 ,
, 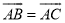 ,
, 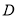 是
是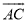 上一点(不与点
上一点(不与点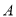 ,
, 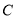 重合),延长
重合),延长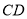 至点
至点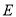 .
.

(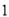 )求证:
)求证: 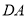 平分
平分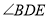 .
.
(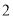 )若
)若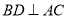 于点
于点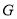 ,
, 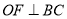 于点
于点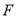 ,求证:
,求证: 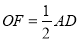 .
.
查看答案和解析>>
科目: 来源:浙江省杭州市2018届九年级上学期期中考试数学试卷(含解析) 题型:解答题
已知二次函数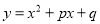 图象的顶点
图象的顶点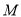 为直线
为直线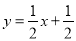 与
与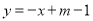 的交点.
的交点.
(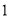 )用含
)用含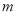 的代数式来表示顶点
的代数式来表示顶点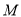 的坐标.
的坐标.
(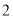 )当
)当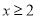 时,二次函数
时,二次函数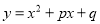 与
与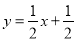 的值均随
的值均随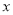 的增大而增大,求
的增大而增大,求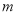 的取值范围.
的取值范围.
(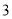 )若
)若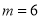 ,当
,当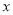 取值为
取值为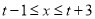 时,二次函数
时,二次函数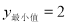 ,求
,求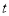 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com