
科目: 来源:2017年陕西师大附中中考数学二模试卷 题型:解答题
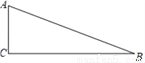
如图,已知△ABC,∠C=90°.请用尺规作一个正方形,使C为正方形的一个顶角,其余三个顶点分别在AB、BC、AC边上.(保留作图痕迹,不写作法)
查看答案和解析>>
科目: 来源:2017年陕西师大附中中考数学二模试卷 题型:解答题
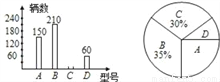
某课题小组为了了解某品牌电动自行车的销售情况,对某专卖店第一季度该品牌A、B、C、D四种型号的销售做了统计,绘制成如下两幅统计图(均不完整)
(1)该店第一季度售出这种品牌的电动自行车共多少辆?
(2)把两幅统计图补充完整;
(3)若该专卖店计划订购这四款型号的电动自行车1800辆,求C型电动自行车应订购多少辆?
查看答案和解析>>
科目: 来源:2017年陕西师大附中中考数学二模试卷 题型:解答题
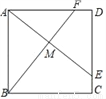
如图,正方形ABCD中,E、F分别是边CD、DA上的点,且CE=DF,AE与BF交于点M.求证:AE⊥BF.
查看答案和解析>>
科目: 来源:2017年陕西师大附中中考数学二模试卷 题型:解答题
芜湖长江大桥是中国跨度最大的公路和铁路两用桥梁,大桥采用低塔斜拉桥桥型(如甲图),图乙是从图甲引申出的平面图,假设你站在桥上测得拉索AB与水平桥面的夹角是30°,拉索CD与水平桥面的夹角是60°,两拉索顶端的距离BC为2米,两拉索底端距离AD为20米,请求出立柱BH的长.(结果精确到0.1米, 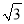 ≈1.732)
≈1.732)
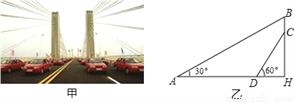
查看答案和解析>>
科目: 来源:2017年陕西师大附中中考数学二模试卷 题型:解答题
某工厂生产一种产品,当生产数量至少为10吨,但不超过50吨时,每吨的成本y(万元/吨)与生产数量x(吨)的函数关系的图象如图所示.
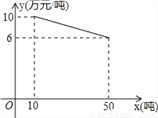
(1)求y关于x的函数解析式,并写出x的取值范围;
(2)当生产这种产品每吨的成本为7万元时,求该产品的生产数量.
(1)y=﹣x+11(10≤x≤50);(2)每吨成本为7万元时,该产品的生产数量40吨. 【解析】试题分析:(1)设y=kx+b(k≠0),然后利用待定系数法求一次函数解析式解答; (2)把y=7代入函数关系式计算即可得解. 试题解析:(1)设y=kx+b(k≠0), 由图可知,函数图象经过点(10,10),(50,6),则 , 解得. 故y=﹣x+11...查看答案和解析>>
科目: 来源:2017年陕西师大附中中考数学二模试卷 题型:解答题
为了提高足球基本功,甲、乙、丙三位同学进行足球传球训练,球从一个人脚下随机传到另一个人脚下,且每位传球人传球给其余两人的机会是均等的,由甲开始传球,共传三次.
(1)请用树状图列举出三次传球的所有可能情况;
(2)三次传球后,球回到甲脚下的概率大还是传到乙脚下的概率大?
(1)、答案见解析;(2)、球回到乙脚下的概率大 【解析】 试题分析:(1)、根据题意画出树状图即可;(2)、根据(1)的树形图,利用概率公式列式进行计算即可得解,分别求出球回到甲脚下的概率和传到乙脚下的概率,比较大小即可. 试题解析:(1)、根据题意画出树状图如下: 由树形图可知三次传球有8种等可能结果; (2)、由(1)可知三次传球后,球回到甲脚下的概率==;传到...查看答案和解析>>
科目: 来源:2017年陕西师大附中中考数学二模试卷 题型:解答题
如图,AD是圆O的切线,切点为A,AB是圆O的弦。过点B作BC//AD,交圆O于点C,连接AC,过点C作CD//AB,交AD于点D。连接AO并延长交BC于点M,交过点C的直线于点P,且?BCP=?ACD。
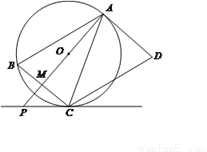
(1) 判断直线PC与圆O的位置关系,并说明理由:
(2) 若AB=9,BC=6,求PC的长。
(1)相切;证明见解析;(2). 【解析】试题分析:(1)通过分析,直线与圆O已经有一个公共点,连接半径0C,只要证明OC⊥PC即可;(2)根据AD是切线和AD∥BC证明AP⊥BC,利用垂径定理计算出CM=BM=3,在Rt△AMB中,利用勾股定义计算出AM的长,在Rt△OMC中,利用勾股定理建立方程计算出圆O的半径的长,最后证明△OMC~△OCP,利用相似三角形的对应边成比例计算出PC的长....查看答案和解析>>
科目: 来源:2017年陕西师大附中中考数学二模试卷 题型:解答题
如图,在平面直角坐标系xOy中,直线y=x+4与坐标轴分别交于A、B两点,抛物线y=﹣x2+bx+c过A、B两点,点D为线段AB上一动点,过点D作CD⊥x轴于点C,交抛物线于点E.
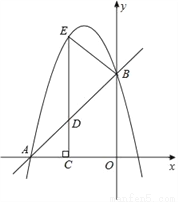
(1)求抛物线的解析式.
(2)求△ABE面积的最大值.
(3)连接BE,是否存在点D,使得△DBE和△DAC相似?若存在,求出点D坐标;若不存在,说明理由.
(1)y=﹣x2﹣3x+4.(2)△ABE面积的最大值为8.(3)存在点D,使得△DBE和△DAC相似,点D的坐标为(﹣3,1)或(﹣2,2). 【解析】试题分析:(1)首先求出点A、B的坐标,然后利用待定系数法求出抛物线的解析式; (2)设点C坐标为(m,0)(m<0),则点E坐标为(m,-m2-3m+4),从而得出OC=-m、OF=-m2-3m+4、BF=-m2-3m,根据S△AB...查看答案和解析>>
科目: 来源:2017年陕西师大附中中考数学二模试卷 题型:解答题
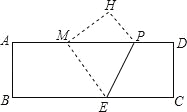
如图,在矩形纸片ABCD中,AB=4,AD=12,将矩形纸片折叠,使点C落在AD边上的点M处,折痕为PE,此时PD=3.
(1)求MP的值;
(2)在AB边上有一个动点F,且不与点A,B重合.当AF等于多少时,△MEF的周长最小?
(3)若点G,Q是AB边上的两个动点,且不与点A,B重合,GQ=2.当四边形MEQG的周长最小时,求最小周长值.(计算结果保留根号)
查看答案和解析>>
科目: 来源:2017年河北省中考数学模拟试卷 题型:单选题
在﹣2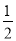 、+
、+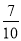 、﹣3、2、0、4、5、﹣1中,负数有( )
、﹣3、2、0、4、5、﹣1中,负数有( )
A. 1个 B. 2个 C. 3个 D. 4个
C 【解析】在﹣2 、+、﹣3、2、0、4、5、﹣1 中,负数有﹣2、﹣3、﹣1 ,共 3 个. 故选C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com