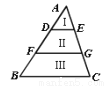
如图,AD=DF=FB,DE∥FG∥BC,则SⅠ:SⅡ:SⅢ=________.

1:3:5 【解析】∵DE∥FG∥BC， ∴△ADE∽△AFG∽△ABC， ∵AD=DF=FB， ∴AD:AF:AB=1:2:3， ∴ =1:4:9， ∴SⅠ:SⅡ:SⅢ=1:3:5. 故答案为：1:3:5.

计算：sin60°+|﹣5|﹣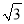 (4015﹣π)0+(﹣1)2017+(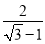)﹣1．

3.5 【解析】试题分析：原式利用零指数幂、负整数指数幂法则，二次根式性质，绝对值的意义以及特殊角的三角函数值计算即可得到结果． 试题解析：原式= =3.5.

解方程：x2+x-1=0

【解析】试题分析：本题考查了求根公式法解一元二次方程组，先确定a=1，b=1，c=-1，然后求出b2-4ac的值，最后代入求出方程的根. 【解析】 a=1，b=1，c=-1． b2-4ac=12-4×1×（-1）=1+4=5． x= （4分） x= x1=，x2=

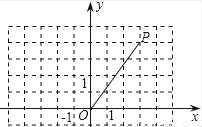
如图，在直角坐标系中，点P的坐标为（3，4），将OP绕原点O逆时针旋转90°得到线段OP′．

（1）在图中画出线段OP′；

（2）求P′的坐标和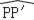的长度．

（1）见解析；（2）P′（﹣4，3），=. 【解析】试题分析： （1）根据旋转的定义画图； （2）根据旋转的性质可得点P′的坐标，由弧长的计算公式可得弧PP′的长. 试题解析： （1）如图： （2）根据旋转的性质可得P′（﹣4，3）， 由弧长公式可得，弧PP′的长度=．

将抛物线y=x2﹣4x+4沿y轴向下平移9个单位，所得新抛物线与x轴正半轴交于点B，与y轴交于点C，顶点为D．求：（1）点B、C、D坐标；（2）△BCD的面积．

（1）（5，0）；（2）15. 【解析】试题分析： （1）先由图象平移的规律求出抛物线的解析式，配方后可得顶点D的坐标，设y=0，可得B的坐标，设x=0，可得C的坐标； （2）过D作DA⊥y轴于点A，根据图形的面积的和与差求△BCD的面积. 试题解析： （1）抛物线y=x2﹣4x+4沿y轴向下平移9个单位后解析式是y=x2﹣4x+4﹣9，即y=x2﹣4x﹣5． ...

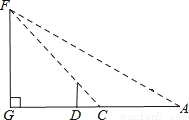
小明是个爱动脑筋的学生，在学习了解直角三角形以后，一天他去测量学校的旗杆GF的高度，此时过旗杆的顶点F的阳光刚好过身高DE为1.6米的小明的头顶且在他身后形成的影长DC=2米．

（1）若旗杆的高度FG是a米，用含a的代数式表示DG．

（2）小明从点C后退6米在A的测得旗杆顶点F的仰角为30°，求旗杆FG的高度．（点A、C、D、G在一条直线上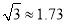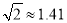， ， ，结果精确到0.1）

（1）a-2；（2）旗杆GF的高度约12.5米． 【解析】试题分析： （1）根据△CDE∽△CGF先求得CG的长，再求DG； （2）先用FG表示出AG的长，再在Rt△AFG中用∠A=30°，借助三角形函数列方程求解. 试题解析： 【解析】 （1）∵由题意知，FG∥DE， ∴△CDE∽△CGF， ∴，即， ∴GD=a-2； （2）如图所示： ...

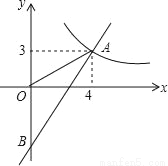
如图，一次函数y=kx+b的图象分别与反比例函数y=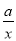的图象在第一象限交于点A（4，3），与y轴的负半轴交于点B，且OA=OB．

（1）求函数y=kx+b和y=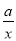的表达式；

（2）已知点C（0，5），试在该一次函数图象上确定一点M，使得MB=MC，求此时点M的坐标．

（1）y=， y=2x﹣5；（2）点M的坐标为（2.5，0）． 【解析】（1）利用待定系数法即可解答； （2）设点M的坐标为（x，2x﹣5），根据MB=MC，得到，即可解答． （1）把点A（4,3）代入函数y=得：a=3×4=12，∴y=．OA==5， ∵OA=OB，∴OB=5，∴点B的坐标为（0，﹣5）， 把B（0，﹣5），A（4，3）代入y=kx+b得：解得：∴y...

一袋中装有形状大小都相同的四个小球，每个小球上各标有一个数字，分别是1，4，7，8．现规定从袋中任取一个小球，对应的数字作为一个两位数的个位数；然后将小球放回袋中并搅拌均匀，再任取一个小球，对应的数字作为这个两位数的十位数．

（1）写出按上述规定得到所有可能的两位数；

（2）从这些两位数中任取一个，求其算术平方根大于4且小于7的概率．

（1）16种等可能的结果数，它们是：11，41，71，81，14，44，74，84，17，47，77，87，18，48，78，88；（2） 【解析】（1）画树状图： 共有16种等可能的结果数，它们是：11，41，71，81，14，44，74，84，17，47，77，87，18，48，78，88； （2）算术平方根大于4且小于7的结果数为6， 所以算术平方根大于4且小于7的概...

如图,抛物线y=ax2+bx+c的顶点为M（﹣2,﹣4），与x轴交于A、B两点,且A（﹣6,0），与y轴交于点C．

（1）求抛物线的函数解析式；

（2）求△ABC的面积；

（3）能否在抛物线第三象限的图象上找到一点P,使△APC的面积最大？若能,请求出点P的坐标；若不能，请说明理由．

（1）y=x2+x﹣3；（2）12；（3）当x=﹣3时，S△APC有最大值，此时点P的坐标是P（﹣3，﹣）． 【解析】试题分析：（1）根据顶点坐标公式即可求得a、b、c的值，即可解题；（2）易求得点B、C的坐标，即可求得OC的长，即可求得△ABC的面积，即可解题；（3）作PE⊥x轴于点E，交AC于点F，可将△APC的面积转化为△AFP和△CFP的面积之和，而这两个三角形有共同的底PF，这一个...

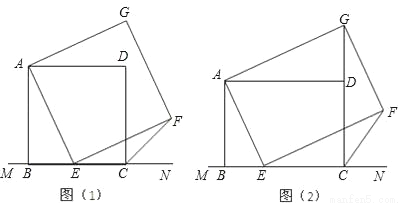
如图（1），已知正方形ABCD在直线MN的上方，BC在直线MN上，E是BC上一点，以AE为边在直线MN的上方作正方形AEFG．

（1）连接GD，求证：△ADG≌△ABE；

（2）连接FC，观察并猜测∠FCN的度数，并说明理由；

（3）如图（2），将图（1）中正方形ABCD改为矩形ABCD，AB=a，BC=b（a、b为常数），E是线段BC上一动点（不含端点B、C），以AE为边在直线MN的上方作矩形AEFG，使顶点G恰好落在射线CD上．判断当点E由B向C运动时，∠FCN的大小是否总保持不变？若∠FCN的大小不变，请用含a、b的代数式表示tan∠FCN的值；若∠FCN的大小发生改变，请举例说明．

（1）见解析；（2）45°；（3）. 【解析】试题分析： （1）由正方形的性质，用SAS证明△BAE≌△DAG； （2）作FH⊥MN于H，证明△EFH≌△ABE，再证△CHF是等腰直角三角形； （3）结合（1）（2），可证明△EFH≌△GAD，△EFH∽△ABE，再用相似三角形的性质得到结论. 试题解析： （1）证明：∵四边形ABCD和四边形AEFG是正方形， ...