
科目: 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷(二) 题型:填空题
如图,双曲线y=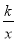 经过Rt△OMN斜边上的点A,与直角边MN相交于点B,已知OA=2AN,△OAB的面积为6,则k的值是_____.
经过Rt△OMN斜边上的点A,与直角边MN相交于点B,已知OA=2AN,△OAB的面积为6,则k的值是_____.
查看答案和解析>>
科目: 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷(二) 题型:填空题
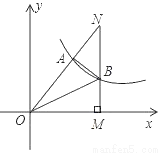
如图,正方形ABCD的边长为1,以对角线AC为边作第二个正方形,再以对角线AE为边作第三个正方形AEGH,如此下去,第n个正方形的边长为_____.
查看答案和解析>>
科目: 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷(二) 题型:解答题
先化简,再求值: 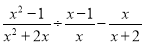 ,其中x满足方程x2+4x﹣5=0.
,其中x满足方程x2+4x﹣5=0.
查看答案和解析>>
科目: 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷(二) 题型:解答题
垃圾的分类处理与回收利用,可以减少污染,节省资源.某城市环保部门为了提高宣传实效,抽样调查了部分居民小区一段时间内生活垃圾的分类情况,其相关信息如下:
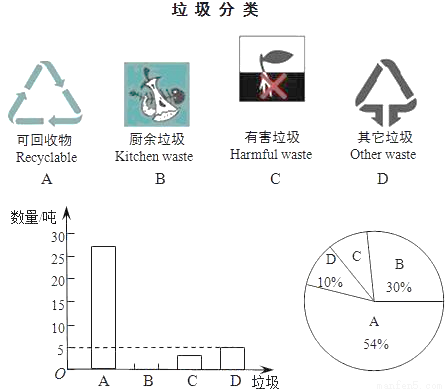
根据图表解答下列问题:
(1)请将条形统计图补充完整;
(2)在抽样数据中,产生的有害垃圾共 吨;
(3)调查发现,在可回收物中塑料类垃圾占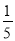 ,每回收1吨塑料类垃圾可获得0.7吨二级原料.假设该城市每月产生的生活垃圾为5 000吨,且全部分类处理,那么每月回收的塑料类垃圾可以获得多少吨二级原料?
,每回收1吨塑料类垃圾可获得0.7吨二级原料.假设该城市每月产生的生活垃圾为5 000吨,且全部分类处理,那么每月回收的塑料类垃圾可以获得多少吨二级原料?
查看答案和解析>>
科目: 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷(二) 题型:解答题
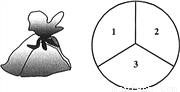
一个不透明的口袋中装有4个完全相同的小球,分别标有数字1,2,3,4,另外有一个可以自由旋转的圆盘,被分成面积相等的3个扇形区域,分别标有数字1,2,3(如图所示).
(1)从口袋中摸出一个小球,所摸球上的数字大于2的概率为 ;
(2)小龙和小东想通过游戏来决定谁代表学校参加歌咏比赛,游戏规则为:一人从口袋中摸出一个小球,另一人转动圆盘,如果所摸球上的数字与圆盘上转出数字之和小于5,那么小龙去;否则小东去.你认为游戏公平吗?请用树状图或列表法说明理由.
查看答案和解析>>
科目: 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷(二) 题型:解答题
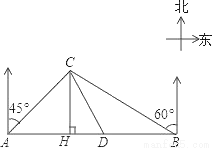
某大草原上有一条笔直的公路,在紧靠公路相距40千米的A、B两地,分别有甲、乙两个医疗站,如图,在A地北偏东45°,B地北偏西60°方向上有一牧民区C,过点C作CH⊥AB于H.
(1)求牧民区C到B地的距离(结果用根式表示);
(2)一天,乙医疗队的医生要到牧民区C出诊,她先由B地搭车沿公路AB到D处(BD<AB)转车,再由D地沿DC方向到牧民区C.若C、D两地距离是B、C两地距离的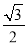 倍,求B、D两地的距离.(结果精确到0.1千米 参考数据:
倍,求B、D两地的距离.(结果精确到0.1千米 参考数据: 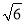 ≈2.449,
≈2.449, 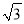 ≈1.732,
≈1.732, 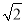 ≈1.414)
≈1.414)
查看答案和解析>>
科目: 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷(二) 题型:解答题
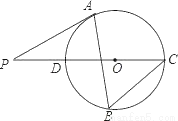
如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.
(1)求证:PA是⊙O的切线;
(2)求证:AC2=CO•CP;
(3)若PD=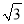 ,求⊙O的直径.
,求⊙O的直径.
查看答案和解析>>
科目: 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷(二) 题型:解答题
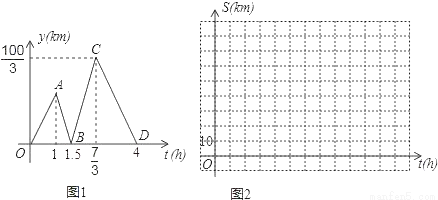
方成同学看到一则材料:甲开汽车,乙骑自行车从M地出发沿一条公路匀速前往N地.设乙行驶的时间为t(h),甲乙两人之间的距离为y(km),y与t的函数关系如图1所示.
方成思考后发现了如图1的部分正确信息:乙先出发1h;甲出发0.5小时与乙相遇.
请你帮助方成同学解决以下问题:
(1)分别求出线段BC,CD所在直线的函数表达式;
(2)当20<y<30时,求t的取值范围;
(3)分别求出甲,乙行驶的路程S甲,S乙与时间t的函数表达式,并在图2所给的直角坐标系中分别画出它们的图象;
(4)丙骑摩托车与乙同时出发,从N地沿同一公路匀速前往M地,若丙经过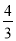 h与乙相遇,问丙出发后多少时间与甲相遇?
h与乙相遇,问丙出发后多少时间与甲相遇?
查看答案和解析>>
科目: 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷(二) 题型:解答题
问题背景:
如图1:在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°.E,F分别是BC,CD上的点.且∠EAF=60°.探究图中线段BE,EF,FD之间的数量关系.
小王同学探究此问题的方法是,延长FD到点G.使DG=BE.连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是 ;
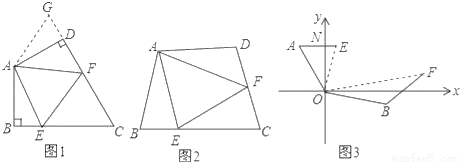
探索延伸:
如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E,F分别是BC,CD上的点,且∠EAF= ∠BAD,上述结论是否仍然成立,并说明理由;
∠BAD,上述结论是否仍然成立,并说明理由;
实际应用:
如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以60海里/小时的速度前进,舰艇乙沿北偏东50°的方向以80海里/小时的速度前进1.5小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,且两舰艇之间的夹角为70°,试求此时两舰艇之间的距离.
问题背景:EF=BE+DF; 探索延伸:结论仍然成立,理由见解析; 实际应用:此时两舰艇之间的距离为210海里. 【解析】【解析】 问题背景:EF=BE+DF; 探索延伸:EF=BE+DF仍然成立. 证明如下:如图,延长FD到G,使DG=BE,连接AG, ∵∠B+∠ADC=180°,∠ADC+∠ADG=180°,∴∠B=∠ADG, 在△ABE和△ADG中...查看答案和解析>>
科目: 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷(二) 题型:解答题
(14分)如图,在平面直角坐标系中,矩形OCDE的三个顶点分别是C(3,0),D(3,4),E(0,4).点A在DE上,以A为顶点的抛物线过点C,且对称轴x=1交x轴于点B.连接EC,AC.点P,Q为动点,设运动时间为t秒.
(1)填空:点A坐标为 ;抛物线的解析式为 .
(2)在图①中,若点P在线段OC上从点O向点C以1个单位/秒的速度运动,同时,点Q在线段CE上从点C向点E以2个单位/秒的速度运动,当一个点到达终点时,另一个点随之停止运动.当t为何值时,△PCQ为直角三角形?
(3)在图②中,若点P在对称轴上从点A开始向点B以1个单位/秒的速度运动,过点P做PF⊥AB,交AC于点F,过点F作FG⊥AD于点G,交抛物线于点Q,连接AQ,CQ.当t为何值时,△ACQ的面积最大?最大值是多少?
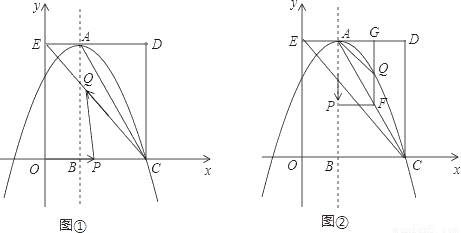
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com