
科目: 来源:2017年广西防城港市中考数学模拟试卷 题型:填空题
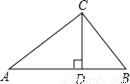
如图,△ABC中,CD⊥AB,垂足为D.下列条件中,能证明△ABC是直角三角形的有 (多选、错选不得分).
①∠A+∠B=90°
②AB2=AC2+BC2
③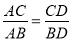
④CD2=AD•BD.
查看答案和解析>>
科目: 来源:2017年广西防城港市中考数学模拟试卷 题型:填空题
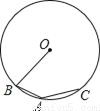
如图,在⊙O中,点A为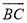 的中点,若∠BAC=140°,则∠OBA的度数为 .
的中点,若∠BAC=140°,则∠OBA的度数为 .
查看答案和解析>>
科目: 来源:2017年广西防城港市中考数学模拟试卷 题型:填空题
将一些半径相同的小圆按如图所示的规律摆放,请仔细观察,第n个图形有 _________个小圆(用含n的代数式表示)

查看答案和解析>>
科目: 来源:2017年广西防城港市中考数学模拟试卷 题型:解答题
计算:tan30°cos60°+tan45°cos30°.
. 【解析】试题分析:根据特殊角的三角函数值可以计算出tan30°cos60°+tan45°cos30°的值. 【解析】 tan30°cos60°+tan45°cos30° = = =.查看答案和解析>>
科目: 来源:2017年广西防城港市中考数学模拟试卷 题型:解答题
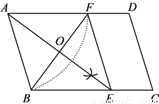
如图:在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线交BC于点E(尺规作图的痕迹保留在图中了), 连接EF.
(1)求证:四边形ABEF为菱形;
(2)AE,BF相交于点O,若BF=6,AB=5,求AE的长.
查看答案和解析>>
科目: 来源:2017年广西防城港市中考数学模拟试卷 题型:解答题
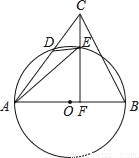
如图,在△ABC中,AB是⊙O的直径,AC与⊙O交于点D,点E在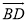 上,连接DE,AE,连接CE并延长交AB于点F,∠AED=∠ACF.
上,连接DE,AE,连接CE并延长交AB于点F,∠AED=∠ACF.
(1)求证:CF⊥AB;
(2)若CD=4,CB=4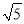 ,cos∠ACF=
,cos∠ACF=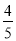 ,求EF的长.
,求EF的长.
查看答案和解析>>
科目: 来源:2017年广西防城港市中考数学模拟试卷 题型:解答题
为了更好改善河流的水质,治污公司决定购买10台污水处理设备.现有A,B两种型号的设备,其中每台的价格,月处理污水量如下表:经调查:购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元.
A型 | B型 | |
价格(万元/台) | a | b |
处理污水量(吨/月) | 240 | 180 |
(1)求a,b的值;
(2)治污公司经预算购买污水处理设备的资金不超过105万元,你认为该公司有哪几种购买方案;
(3)在(2)的条件下,若每月要求处理污水量不低于2040吨,为了节约资金,请你为治污公司设计一种最省钱的购买方案.
(1) a的值为12,b的值为10;(2) 所有购买方案为:当A型号为0,B型号为10台;当A型号为1台,B型号为9台;当A型号为2台,B型号为8台;有3种购买方案;(3) 公司最省钱的一种购买方案为:购买A型处理机1台,B型处理机9台. 【解析】试题分析:(1)购买A型的价格是a万元,购买B型的设备b万元,根据购买一台A型号设备比购买一台B型号设备多2万元,购买2台A型设备比购买3台B型号...查看答案和解析>>
科目: 来源:2017年广西防城港市中考数学模拟试卷 题型:解答题
如图,某办公楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,办公楼在建筑物的墙上留下高2米的影子CE,而当光线与地面夹角是45°时,办公楼顶A在地面上的影子F与墙角C有25米的距离(B,F,C在一条直线上).
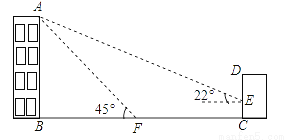
(1)求办公楼AB的高度;
(2)若要在A,E之间挂一些彩旗,请你求出A,E之间的距离.
(参考数据:sin22°≈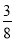 ,cos22°≈
,cos22°≈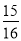 ,tan22°≈
,tan22°≈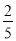 )
)
查看答案和解析>>
科目: 来源:2017年广西防城港市中考数学模拟试卷 题型:解答题
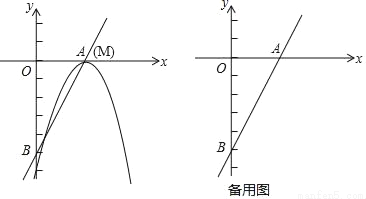
已知直线y=2x﹣5与x轴和y轴分别交于点A和点B,抛物线y=﹣x2+bx+c的顶点M在直线AB上,且抛物线与直线AB的另一个交点为N.
(1)如图,当点M与点A重合时,求抛物线的解析式;
(2)在(1)的条件下,求点N的坐标和线段MN的长;
(3)抛物线y=﹣x2+bx+c在直线AB上平移,是否存在点M,使得△OMN与△AOB相似?若存在,直接写出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com