
科目: 来源:浙江省金华市2017-2018学年八年级上册期末模拟数学试卷 题型:解答题
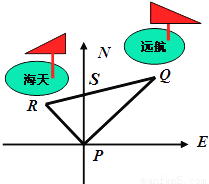
某港口位于东西方向的海岸线上.“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里.它们离开港口一个半小时后相距30海里.如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行?为什么?
查看答案和解析>>
科目: 来源:浙江省金华市2017-2018学年八年级上册期末模拟数学试卷 题型:解答题
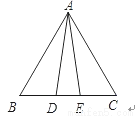
已知:如图,D、E是△ABC中BC边上的两点,AD=AE,要证明△ABE≌△ACD,应该再增加一个什么条件?请你增加这个条件后再给予证明.
查看答案和解析>>
科目: 来源:浙江省金华市2017-2018学年八年级上册期末模拟数学试卷 题型:解答题
如果关于x的不等式|x﹣2|+|x+3|≥a对于x取任意数都成立,则a的取值范围是多少?并说明理由.
a≤5 【解析】试题分析:根据线段上的点到线两端点的距离的和最小,可得答案. 试题分析:∵|x﹣2|+|x+3|≥5, ∴关于x的不等式|x﹣2|+|x+3|≥a对于x取任意数都成立, a≤5.查看答案和解析>>
科目: 来源:浙江省金华市2017-2018学年八年级上册期末模拟数学试卷 题型:解答题
能不能找到这样的a值,使关于x的不等式(1﹣a)x>a﹣5的解集是x<2.
能找到这样的a值,使关于x的不等式(1﹣a)x>a﹣5的解集是x<2 【解析】试题分析:根据已知不等式的解集得出1﹣a<0, =2,求出方程的解即可. 试题解析:∵关于x的不等式(1﹣a)x>a﹣5的解集是x<2, ∴1﹣a<0, =2, 解得:a=, 经检验a=是方程=2的解, 即能找到这样的a值,使关于x的不等式(1﹣a)x>a﹣5的解集是x<2.查看答案和解析>>
科目: 来源:浙江省金华市2017-2018学年八年级上册期末模拟数学试卷 题型:解答题
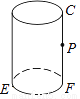
如图:有一个圆柱,底面圆的直径EF=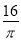 ,高FC=12cm,P为FC的中点,求蚂蚁从E点爬到P点的最短距离是多少?(画出平面图形)
,高FC=12cm,P为FC的中点,求蚂蚁从E点爬到P点的最短距离是多少?(画出平面图形)
查看答案和解析>>
科目: 来源:浙江省金华市2017-2018学年八年级上册期末模拟数学试卷 题型:解答题
李老师每天坚持晨跑.下图反映的是李老师某天6:20从家出发小跑到赵化北门,在北门休息几分钟后又慢跑回家的函数图象. 其中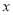 (分钟)表示所用时间,
(分钟)表示所用时间, 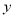 (千米)表示李欢离家的距离.
(千米)表示李欢离家的距离.
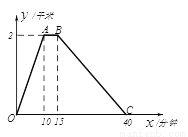
(1)分别求出线段0≤x≤10和15≤x≤40的函数解析式?
(2)李老师在这次晨跑过程中什么时间距离家500米?
(1)当0≤x≤10时,y=0.1x;当15≤x≤40时,y=3.2-0.08x; (2)李老师在这次晨跑过程中分别于5分、33.75分距离家500米。 【解析】试题分析:(1)利用待定系数法即可求得;(2)求出OA的解析式,然后根据OA、BC的解析式,利用y=0.5千米计算求出相应的x的值,再加上6点20分即可. 试题解析:(1)设OA的解析式为y1=kx, 则10k=2...查看答案和解析>>
科目: 来源:浙江杭州下城区启正中学2017-2018学年八年级上学期中考试数学试卷(含解析) 题型:单选题
点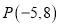 关于
关于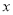 轴的对称点在( ).
轴的对称点在( ).
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
C 【解析】∵点P(-5,8)在第二象限, ∴点P关于x 的对称点在第三象限. 故选C.查看答案和解析>>
科目: 来源:浙江杭州下城区启正中学2017-2018学年八年级上学期中考试数学试卷(含解析) 题型:单选题
下列判断正确的是( ).
A. 有一直角边相等的两个直角三角形全等 B. 斜边相等的两个等腰直角三角形全等
C. 腰相等的两个等腰三角形全等 D. 两个锐角对应相等的两个直角三角形全等
B 【解析】A选项中,因为一条直角边相等时,另两条边的大小关系并不确定,所以不能确定两三角形是否全等,所以A中说法错误; B选项中,斜边相等的两个等腰直角三角形全等,因为此时两直角边一定相等,所以B中说法正确; C选项中,腰相等的两个等腰三角形的顶角不一定相等,因此不能确定这样的等腰三角形全等,所以C中说法错误; D选项中,两个锐角对应相等的两个直角三角形不一定全等,因为两...查看答案和解析>>
科目: 来源:浙江杭州下城区启正中学2017-2018学年八年级上学期中考试数学试卷(含解析) 题型:单选题
已知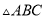 中,
中, 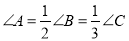 ,则它的三条边之比为( ).
,则它的三条边之比为( ).
A. 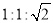 B.
B. 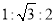 C.
C.  D.
D. 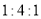
查看答案和解析>>
科目: 来源:浙江杭州下城区启正中学2017-2018学年八年级上学期中考试数学试卷(含解析) 题型:单选题
下列定理中,没有逆定理的是( ).
A. 全等三角形对应角相等 B. 线段垂直平分线上的点到线段两端的距离相等
C. 一个三角形中,等角对等边 D. 两直线平行,同位角相等
A 【解析】A选项中,因为“对应角相等不一定是全等三角形”,所以A中定理没有有逆定理; B选项中,因为“到线段两端距离相等的点在线段的垂直平分线上”,所以B中定理有逆定理; C选项中,因为“在同一个三角形中,等边对等角”,所以C中定理有逆定理; D选项中,因为“同位角相等,两直线平行”,所以D中定理有逆定理. 故选A.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com