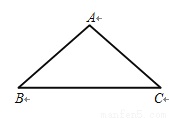
已知△ABC的三边长分别为4、4、6，在△ABC所在平面内画一条直线，将△ABC

分割成两个三角形，使其中的一个是等腰三角形，则这样的直线最多可画 _______条．

4 【解析】试题解析：如图所示： 当AC=CD=4，AB=BG=4，AF=CF，AE=BE时，都能得到符合题意的等腰三角形。 故答案为：4.

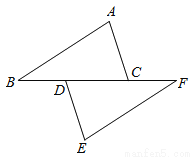
已知：如图，点D，C在BF上，且BD=CF，∠B=∠F，∠A=∠E． 求证：△ABC≌△EFD．

见解析 【解析】试题分析：依据证明△ABC≌△EFD． 试题解析：∵BD=CF， ∴BD+CD=CF+CD， 即， 在和中， ， ∴

已知：如图，在△ABC中，AB=AC，点D、E分别在AB、AC上，且DE∥BC．求证：AD=AE．

见解析 【解析】试题分析：在△ABC中，AB=AC，依据等边对等角，得，依据DE∥BC， ， ，推出，可以判定AD=AE． 试题解析：在△ABC中， ∵ ∴， ∵， ∴， ， ∴， ∴．

如图，在4×4的正方形网格中，每个小正方形的顶点称为格点，每个小正方形的边长均为1．在图①，图②中已画出线段AB，在图③中已画出点A．按下列要

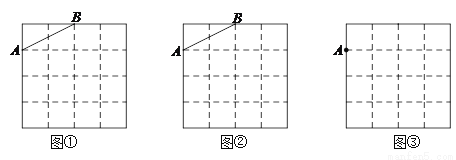
求画图：

（1）在图①中，以格点为顶点，AB为一边画一个等腰三角形ABC；

（2）在图②中，以格点为顶点，AB为一边画一个正方形；

（3）在图③中，以点A为一个顶点，另外三个顶点也在格点上，画一个面积最大的正方

形，这个正方形的面积= ．

（1）见解析；（2）见解析；（3）10 【解析】试题分析：（1）根据勾股定理，结合网格结构，作出两边分别为的等腰三角形即可； （2）根据勾股定理逆定理，结合网格结构，作出边长为的正方形； （3）根据勾股定理逆定理，结合网格结构，作出最长的线段作为正方形的边长即可． 试题解析：(1)如图①，符合条件的C点有5个： (2)如图②，正方形ABCD即为满足条件的图形： ； ...

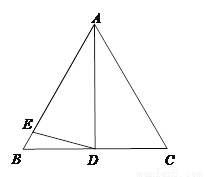
如图，AD是等边三角形ABC的中线，E是AB上的点，且AE=AD， 求∠EDB的度数．

15° 【解析】试题分析：由AD是等边△ABC的中线，根据等边三角形中：三线合一的性质，即可求得 又由 根据等边对等角与三角形内角和定理，即可求得的度数，继而求得答案． 试题解析：∵AD是等边△ABC的中线， ∴AD⊥BC，∠BAD=∠BAC=60°=30°， ∴∠ADB=90°. ∵AE=AD. ∴∠ADE=∠AED==75°. ∴∠EDB=∠ADB-∠...

如图，△ABC中，AB=AC，AB的垂直平分线交AB于点N，交AC于点M．连 接MB，若AB＝8 cm，△MBC的周长是14 cm．

(1)求BC的长；

(2)在直线MN上是否存在点P，使PB+CP的值最小？若存在，直接写出PB+CP的最小值；若不存在，说明理由．

（1）6；（2）8 【解析】试题分析： 根据垂直平分线的性质，可得与的关系，再根据三角形的周长，可得答案； 根据两点之间线段最短，可得点与点的关系，可得与的关系． 试题解析： ∵MN是AB的垂直平分线 ∴MA=MB， ∵， ， = , 即 ∴. 当点与点重合时，PB+CP的值最小，PB+CP能取到的最小值=8．

如图，AB为一棵大树(垂直于地面，即AB⊥BC)，在树上距地面12m的D处有两只猴子，它们同时发现地面上的C处有一筐水果，一只猴子从D处向上爬到树顶A处，再利用拉在A处的滑绳AC，滑到C处，另一只猴子从D处滑到地面B，再由B跑到C，已知两猴子经过的路程都是20m，求树高AB．

15m 【解析】试题分析：设AD长为x m，则AC=(20-x) m，得出，依据勾股定理列出方程，解出的值，即可求出树的高度. 试题解析：设AD长为x m，则AC=(20-x) m， BC=20-12=8 m, 在Rt△ABC中，由勾股定理得 , ∴, 解得. ∴AB=AD+BD=3+12=15. 答：树的高度为15 m.

如图，△ABC中，AD是高，CE是中线，点G是CE的中点，DG⊥CE，点G为垂足．

（1）求证：DC=BE；

（2）若∠AEC=66°，求∠BCE的度数．

(1）证明见机械；（2)22° 【解析】试题分析： 由是的中点， 得到是的垂直平分线，根据线段垂直平分线的性质得到由是的斜边上的中线，根据直角三角形斜边上的中线等于斜边的一半得到 即可得到 由得到，由得到 根据三角形外角性质得到 则 由此根据外角的性质来求的度数． 试题解析： 如图，∵是的中点， ∴是的垂直平分线， ∴ ∵是高， 是中线， ∴是的斜边上的中...

如图①，美丽的弦图，蕴含着四个全等的直角三角形．

(1)弦图中包含了一大，一小两个正方形，已知每个直角三角形较长的直角边为，较短的直角边为，斜边长为，试利用图①验证勾股定理；

(2)如图②，将这四个全等的直角三角形紧密地拼接，形成飞镖状，已知外围轮廓（实线）的周长为， ，求该飞镖状图案的面积；

(3)如图③，将八个全等的直角三角形紧密地拼接，记图中正方形，正方形，正方形的面积分别为， ， ，若，则=________．

（1）见解析；（2）24；（3） 【解析】（1）通过图中小正方形面积证明勾股定理； （2）可设 根据勾股定理列出方程可求，再根据直角三角形面积公式计算即可求解； （3）根据图形的特征得出四边形的面积设为，将其余八个全等的三角形面积一个设为，从而用表示出得出答案即可． 试题解析：（） . （）由题意知， ， ． 设，那么， 在中， ，解得. 该飞镖状图案的面积...

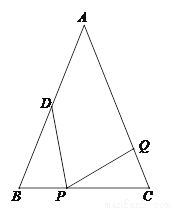
如图，已知△ABC中，AB=AC=6cm，BC=4cm，点D为AB的中点．

⑴如果点P在线段BC上以1cm/s的速度由点B向点C运动，同时，点Q在线段CA上由点C向点A运动．

①若点Q的运动速度与点P的运动速度相等，经过1秒后，△BPD与△CPQ是否全等，请说明理由；

②若点Q的运动速度与点P的运动速度不相等，当点Q的运动速度为______cm/s时，在某一时刻也能够使△BPD与△CPQ全等．

⑵若点Q以②中的运动速度从点C出发，点P以原来的运动速度从点B同时出发，都按逆时针方向沿△ABC的三边运动．求经过多少秒后，点P与点Q第一次相遇，并写出第一次相遇点在△ABC的哪条边上？

（1）①全等，理由见解析；②1.5（2）经过24秒点P与点Q第一次在边AC上相遇 【解析】试题分析：（1）①根据时间和速度分别求得两个三角形中的边的长，根据 判定两个三角形全等． ②根据全等三角形应满足的条件探求边之间的关系，再根据路程=速度×时间公式，先求得点运动的时间，再求得点的运动速度； （2）根据题意结合图形分析发现：由于点的速度快，且在点的前边，所以要想第一次相遇，则应该比点多...