
科目: 来源:四川省南充市营山县城南二小2017-2018学年上学期九年级数学期末质量检测试卷 题型:解答题
已知关于x的一元二次方程x2+(2m+1)x+m2-4=0.
(1)当m为何值时,方程有两个不相等的实数根?
(2)若边长为5的菱形的两条对角线的长分别为方程两根的2倍,求m的值.
(1)当m>-时,方程有两个不相等的实数根;(2)m的值为-4. 【解析】试题分析:(1)根据方程的系数结合根的判别式,即可得出解之即可得出结论; (2)设方程的两根分别为 根据根与系数的关系结合菱形的性质,即可得出关于 的一元二次方程,解之即可得出的值,再根据即可确定的值. 试题解析:(1)∵方程有两个不相等的实数根, 解得: ∴当时,方程有两个不相等的实数根. ...查看答案和解析>>
科目: 来源:四川省南充市营山县城南二小2017-2018学年上学期九年级数学期末质量检测试卷 题型:解答题
某商品的进价为每件40元,售价为每件60元时,每个月可卖出100件;如果每件商品的售价每上涨1元,则每个月少卖2件.设每件商品的售价为x元(x为正整数),每个月的销售利润为y元.
(1)当每件商品的售价是多少元时,每个月的利润刚好是2250元?
(2)当每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?
(1)65或85;(2)当售价定为75时,每个月可获得最大利润,最大的月利润是2450元. 【解析】试题分析:(1)如果每件商品的售价每上涨1元,则每个月少卖2件,可得销售量为100﹣2(x﹣60),销售量乘以利润即可得到等式[100﹣2(x﹣60)](x﹣40)=2250,解答即可; (2)将(1)中的2250换成y即可解答. 试题解析:【解析】 (1)[100﹣2(x﹣60...查看答案和解析>>
科目: 来源:四川省南充市营山县城南二小2017-2018学年上学期九年级数学期末质量检测试卷 题型:解答题
如图,在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按顺时针方向旋转n度后,得到△DEC,点D刚好落在AB边上.
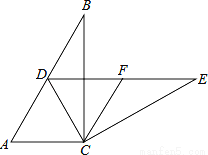
(1)求n的值;
(2)若F是DE的中点,判断四边形ACFD的形状,并说明理由.
(1)60;(2)四边形ACFD是菱形.理由见解析. 【解析】试题分析:(1)、利用旋转的性质得出AC=CD,进而得出△ADC是等边三角形,即可得出∠ACD的度数; (2)、利用直角三角形的性质得出FC=DF,进而得出AD=AC=FC=DF,即可得出答案. 试题解析:(1)、∵在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按顺时针方向旋转n度后,得到△DEC,...查看答案和解析>>
科目: 来源:四川省南充市营山县城南二小2017-2018学年上学期九年级数学期末质量检测试卷 题型:解答题
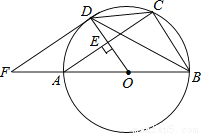
如图,AB是⊙O的直径,OD垂直于弦AC于点E,且交⊙O于点D,F是BA延长线上一点,若∠CDB=∠BFD.
(1)求证:FD是⊙O的一条切线;
(2)若AB=10,AC=8,求DF的长.
查看答案和解析>>
科目: 来源:四川省南充市营山县城南二小2017-2018学年上学期九年级数学期末质量检测试卷 题型:解答题
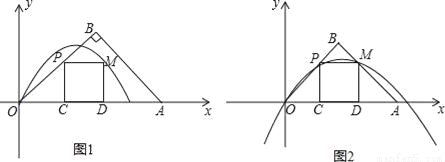
如图1在平面直角坐标系中.等腰Rt△OAB的斜边OA在x轴上.P为线段OB上﹣动点(不与O,B重合).过P点向x轴作垂线.垂足为C.以PC为边在PC的右侧作正方形PCDM.OP=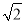 t,OA=3.设过O,M两点的抛物线为y=ax2+bx.其顶点N(m,n)
t,OA=3.设过O,M两点的抛物线为y=ax2+bx.其顶点N(m,n)
(1)写出t的取值范围 ,写出M的坐标:( , );
(2)用含a,t的代数式表示b;
(3)当抛物线开向下,且点M恰好运动到AB边上时(如图2)
①求t的值;
②若N在△OAB的内部及边上,试求a及m的取值范围.
查看答案和解析>>
科目: 来源:四川省南充市营山县城南二小2017-2018学年上学期九年级数学期末质量检测试卷 题型:解答题
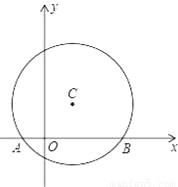
.如图,在平面直角坐标系中,以点C(1,1)为圆心,2为半径作圆,交x轴于A,B两点,点P在优弧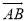 上.
上.
(1)求出A,B两点的坐标;
(2)试确定经过A、B且以点P为顶点的抛物线解析式;
(3)在该抛物线上是否存在一点D,使线段OP与CD互相平分?若存在,求出点D的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源:辽宁省2017-2018学年七年级上学期期末模拟数学试卷 题型:单选题
下列各组数中,相等的是( )
A. –1与(–4)+(–3) B.  与–(–3)
与–(–3)
C.  与
与 D.
D.  与–16
与–16
查看答案和解析>>
科目: 来源:辽宁省2017-2018学年七年级上学期期末模拟数学试卷 题型:单选题
下列平面图形中不能围成正方体的是( )
A. 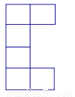 B.
B. 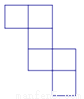 C.
C. 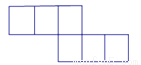 D.
D. 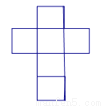
查看答案和解析>>
科目: 来源:辽宁省2017-2018学年七年级上学期期末模拟数学试卷 题型:单选题
由四舍五入法得到的近似数8.8×103,下列说法中正确的是 ( )
A. 精确到十分位 B. 精确到个位 C. 精确到百位 D. 精确到千位
C 【解析】试题解析:个位代表千,那么十分位就代表百, 精确到百位. 故选C.查看答案和解析>>
科目: 来源:辽宁省2017-2018学年七年级上学期期末模拟数学试卷 题型:单选题
在灯塔O处观测到轮船A位于北偏西54°的方向,同时轮船B在南偏东15°的方向,那么∠AOB的大小为( )

A. 69° B. 111° C. 141° D. 159°
C 【解析】试题分析:首先计算出∠3的度数,再计算∠AOB的度数即可. 【解析】 由题意得:∠1=54°,∠2=15°, ∠3=90°﹣54°=36°, ∠AOB=36°+90°+15°=141°, 故选:C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com