
科目: 来源:重庆市校2018届九年级上学期期末模拟数学试卷 题型:解答题
解方程:
(1)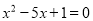 ;
;
(2) .
.
查看答案和解析>>
科目: 来源:重庆市校2018届九年级上学期期末模拟数学试卷 题型:解答题
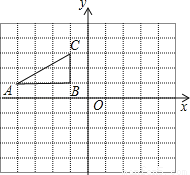
如图,方格纸中的每个小方格都是边长为1个单位的正方形.Rt△ABC的顶点均在格点上,建立平面直角坐标系后,点A的坐标为(﹣4,1),点B的坐标为(﹣1,1).
(1)先将Rt△ABC向右平移5个单位,再向下平移1个单位后得到Rt△A1B1C1.试在图中画出图形Rt△A1B1C1,并写出A1的坐标;
(2)将Rt△A1B1C1绕点A1顺时针旋转90°后得到Rt△A2B2C2,试在图中画出图形Rt△A2B2C2.并计算Rt△A1B1C1在上述旋转过程中C1所经过的路程.
查看答案和解析>>
科目: 来源:重庆市校2018届九年级上学期期末模拟数学试卷 题型:解答题
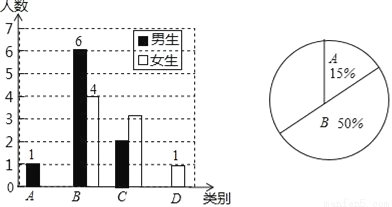
课前预习是学习的重要环节,为了了解所教班级学生完成课前预习的具体情况,某班主任对本班部分学生进行了为期半个月的跟踪调查,他将调查结果分为四类:A.优秀,B.良好,C.一般,D.较差,并将调查结果绘制成以下两幅不完整的统计图.
(1)本次调查的样本容量是 ;其中A类女生有 名,D类学生有 名;
(2)将条形统计图和扇形统计图补充完整;
(3)若从被调查的A类和D类学生中各随机选取一位学生进行“一帮一”辅导学习,即A类学生辅导D类学生,请用列表法或画树状图的方法求出所选两位同学中恰好是一位女同学辅导一位男同学的概率.
查看答案和解析>>
科目: 来源:重庆市校2018届九年级上学期期末模拟数学试卷 题型:解答题
如图,AB是⊙O的直径,点C,D在圆上,且四边形AOCD是平行四边形,过点D作⊙O的切线,分别交OA的延长线与OC的延长线于点E,F,连接BF.

(1)求证:BF是⊙O的切线;
(2)已知圆的半径为1,求EF的长.
(1)证明见解析;(2)EF=2. 【解析】试题分析:(1)、先证明四边形AOCD是菱形,从而得到∠AOD=∠COD=60°,再根据切线的性质得∠FDO=90°,接着证明△FDO≌△FBO得到∠ODF=∠OBF=90°,然后根据切线的判定定理即可得到结论;(2)、在Rt△OBF中,利用60度的正切的定义求解. 试题解析:(1)、连结OD,如图,∵四边形AOCD是平行四边形,而OA=OC...查看答案和解析>>
科目: 来源:重庆市校2018届九年级上学期期末模拟数学试卷 题型:解答题
某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利40元。为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出2件。求:
⑴若商场平均每天要盈利1200元,每件衬衫应降价多少元?
⑵每件衬衫降价多少元,商场平均每天盈利最多,最多盈利是多少元?
(1)20.(2)15,1250. 【解析】试题分析:(1)首先设每件寸衫应降价x元,然后根据总利润=单件利润×数量列出方程进行求解;(2)、根据二次函数的顶点式得出最大值. 试题解析:(1)设每件衬衫应降价x元。 根据题意,得 (40-x)(20+2x)=1200 整理,得x2-30x+200=0 解之得 x1=10,x2=20。 因题意要尽快减少库存,所以x取20。 ...查看答案和解析>>
科目: 来源:重庆市校2018届九年级上学期期末模拟数学试卷 题型:解答题
古希腊的毕达哥拉斯学派由古希腊哲学家毕达哥拉斯所创立,毕达哥拉斯学派认为数是万物的本原,事物的性质是由某种数量关系决定的,如他们研究各种多边形数:记第n个k边形数N(n,k)=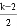 n2+
n2+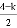 n(n≥1,k≥3,k、n都为整数),
n(n≥1,k≥3,k、n都为整数),
如第1个三角形数N(1,3)=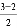 ×12+
×12+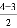 ×1=1;
×1=1;
第2个三角形数N(2,3)=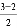 ×22+
×22+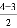 ×2=3;
×2=3;
第3个四边形数N(3,4)=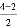 ×32+
×32+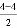 ×3=9;
×3=9;
第4个四边形数N(4,4)=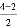 ×42+
×42+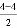 ×4=16.
×4=16.
(1)N(5,3)=________,N(6,5)=________;
(2)若N(m,6)比N(m+2,4)大10,求m的值;
(3)若记y=N(6,t)-N(t,5),试求出y的最大值.
(1)15;51;(2)7;(3)当t=5时,y有最大值,其最大值为16. 【解析】试题分析:(1)根据N(n,k)的定义,求出N(5,3),N(6,5)的值即可. (2)根据N(m,6)比N(m+2,4)大10,列出方程即可解决问题. (3)首先根据y=N(6,t)-N(t,5),构建二次函数,然后根据二次函数的性质即可解决问题. 试题解析:(1)N(5,3)=×52+×5 =...查看答案和解析>>
科目: 来源:重庆市校2018届九年级上学期期末模拟数学试卷 题型:解答题
如图1,在△ACB和△AED中,AC=BC,AE=DE,∠ACB=∠AED=90°,点E在AB上,F是线段BD的中点,连接CE、FE.
(1)若AD=3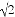 ,BE=4,求EF的长;
,BE=4,求EF的长;
(2)求证:CE=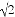 EF;
EF;
(3)将图1中的△AED绕点A顺时针旋转,使AED的一边AE恰好与△ACB的边AC在同一条直线上(如图2),连接BD,取BD的中点F,问(2)中的结论是否仍然成立,并说明理由.

查看答案和解析>>
科目: 来源:重庆市校2018届九年级上学期期末模拟数学试卷 题型:解答题
(14分)如图,已知抛物线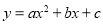 (
(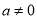 )与x轴交于点A(1,0)和点B(﹣3,0),与y轴交于点C,且OC=OB.
)与x轴交于点A(1,0)和点B(﹣3,0),与y轴交于点C,且OC=OB.
(1)求此抛物线的解析式;
(2)若点E为第二象限抛物线上一动点,连接BE,CE,求四边形BOCE面积的最大值,并求出此时点E的坐标;
(3)点P在抛物线的对称轴上,若线段PA绕点P逆时针旋转90°后,点A的对应点A′恰好也落在此抛物线上,求点P的坐标.
(1);(2)当a=时,S四边形BOCE最大,且最大值为,此时,点E坐标为(,);(3)P(﹣1,1)或(﹣1,﹣2). 【解析】 试题分析:(1)将A、B两点的坐标代入抛物线的解析式中,即可求出二次函数的解析式; (2)过E作EF⊥x轴于F.设E(a,)(﹣3<a<0),则EF=,BF=a+3,OF=﹣a,∴S四边形BOCE==BF•EF+(OC+EF)•OF =,配方即可得出...查看答案和解析>>
科目: 来源:2017年海南省定安县中考数学仿真试卷(二) 题型:单选题
2017的相反数是( )
A. 2017 B. ﹣2017 C.  D. ﹣
D. ﹣
查看答案和解析>>
科目: 来源:2017年海南省定安县中考数学仿真试卷(二) 题型:单选题
若代数式x﹣3的值为2,则x等于( )
A. 1 B. ﹣1 C. 5 D. ﹣5
C 【解析】根据题意得:x﹣3=2,解得:x=5,故选C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com