
科目: 来源:福建省建瓯市2018届九年级数学上册期末测试卷 题型:填空题
已知二次函数y=x2+2mx+2,当x>2时,y的值随x的增大而增大,则实数m的取值范围是 .
m≥-2. 【解析】试题分析:抛物线的对称轴为直线x==﹣m,∵当x>2时,y的值随x值的增大而增大,∴﹣m≤2,解得m≥﹣2.故答案为:m≥﹣2.查看答案和解析>>
科目: 来源:福建省建瓯市2018届九年级数学上册期末测试卷 题型:填空题
一个底面直径是80cm,母线长为90cm的圆锥的侧面展开图的圆心角的度数为 .
160°. 【解析】试题分析:∵圆锥的底面直径是80cm, ∴圆锥的侧面展开扇形的弧长为:πd=80π, ∵母线长90cm, ∴圆锥的侧面展开扇形的面积为: lr=×80π×90=3600π, ∴=3600π, 解得:n=160.查看答案和解析>>
科目: 来源:福建省建瓯市2018届九年级数学上册期末测试卷 题型:填空题
如图,顺次连接圆内接矩形各边的中点,得到菱形ABCD,若BD=10,DF=4,则菱形ABCD的边长为__ __.
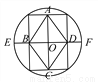
查看答案和解析>>
科目: 来源:福建省建瓯市2018届九年级数学上册期末测试卷 题型:填空题
如图,在四边形ABCD中,∠ABC=90°,AD∥BC,AD=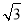 ,以对角线BD为直径的⊙O与CD切于点D,与BC交于点E,∠ABD=30°,则图中阴影部分的面积为___ _.(不取近似值)
,以对角线BD为直径的⊙O与CD切于点D,与BC交于点E,∠ABD=30°,则图中阴影部分的面积为___ _.(不取近似值)
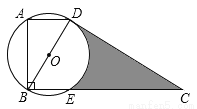
查看答案和解析>>
科目: 来源:福建省建瓯市2018届九年级数学上册期末测试卷 题型:解答题
解方程:(x+1)(x-1)=2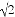 x.
x.
查看答案和解析>>
科目: 来源:福建省建瓯市2018届九年级数学上册期末测试卷 题型:解答题
设x1,x2是关于x的方程x2-4x+k+1=0的两个实数根,是否存在实数k,使得x1x2>x1+x2成立?请说明理由.
不存在 【解析】试题分析:根据方程有实数根结合根的判别式即可得出关于的一元一次不等式,解之即可得出的取值范围,再根据根与系数的关系结合即可得出关于的一元一次不等式,解之即可得出的取值范围,由两个的范围无交集即可得出不存在实数使得成立. 试题解析:不存在. 理由:由题意得 解得 ∵是一元二次方程的两个实数根, 由,得 ∴不存在实数使得成立.查看答案和解析>>
科目: 来源:福建省建瓯市2018届九年级数学上册期末测试卷 题型:解答题
如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-3,2),B(0,4),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;平移△ABC,若点A的对应点A2的坐标为(0,-4),画出平移后对应的△A2B2C2;
(2)若将△A1B1C绕某一点旋转可以得到△A2B2C2,请直接写出旋转中心的坐标;
(3)在x轴上有一点P,使得PA+PB的值最小,请直接写出点P的坐标.
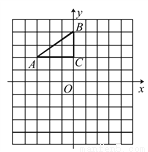
查看答案和解析>>
科目: 来源:福建省建瓯市2018届九年级数学上册期末测试卷 题型:解答题
袋中装有大小相同的2个红球和2个绿球.
(1)先从袋中摸出1个球后放回,混合均匀后再摸出1个球.
①求第一次摸到绿球,第二次摸到红球的概率;
②求两次摸到的球中有1个绿球和1个红球的概率;
(2)先从袋中摸出1个球后不放回,再摸出1个球,则两次摸到的球中有1个绿球和1个红球的概率是多少?请直接写出结果.
(1)①;②;(2). 【解析】试题分析:(1)①首先根据题意画出树状图或列表,然后由图表求得所有等可能的结果与第一次摸到绿球,第二次摸到红球的情况,再利用概率公式即可求得答案. ②首先由①求得两次摸到的球中有1个绿球和1个红球的情况,再利用概率公式即可求得答案. (2)由先从袋中摸出1个球后不放回,再摸出1个球,共有等可能的结果为:4×3=12(种),且两次摸到的球中有1个绿球...查看答案和解析>>
科目: 来源:福建省建瓯市2018届九年级数学上册期末测试卷 题型:解答题
如图,在Rt△ABC中,∠ABC=90°,以AB为直径作半圆⊙O交AC于点D,点E为BC的中点,连接DE.
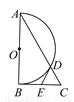
(1)求证:DE是半圆⊙O的切线;
(2)若∠BAC=30°,DE=2,求AD的长.
(1)证明见解析;(2) AD=6. 【解析】试题分析:(1)连接OD,OE,由AB为圆的直径得到三角形BCD为直角三角形,再由E为斜边BC的中点,得到DE=BE=DC,再由OB=OD,OE为公共边,利用SSS得到三角形OBE与三角形ODE全等,由全等三角形的对应角相等得到DE与OD垂直,即可得证; (2)在直角三角形ABC中,由∠BAC=30°,得到BC为AC的一半,根据BC=2DE...查看答案和解析>>
科目: 来源:福建省建瓯市2018届九年级数学上册期末测试卷 题型:解答题
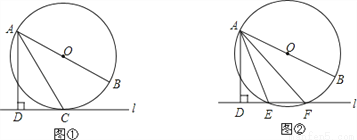
已知直线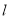 与⊙O,AB是⊙O的直径,AD⊥
与⊙O,AB是⊙O的直径,AD⊥ 于点D.
于点D.
(1)如图①,当直线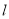 与⊙O相切于点C时,若∠DAC=30°,求∠BAC的大小;
与⊙O相切于点C时,若∠DAC=30°,求∠BAC的大小;
(2)如图②,当直线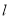 与⊙O相交于点E、F时,若∠DAE=18°,求∠BAF的大小.
与⊙O相交于点E、F时,若∠DAE=18°,求∠BAF的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com