
科目: 来源:2017-2018学年江苏省苏州市初三上期中模拟数学试卷 题型:解答题
解下列方程:(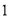 )
)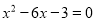 ;(
;(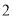 )
) .
.
查看答案和解析>>
科目: 来源:2017-2018学年江苏省苏州市初三上期中模拟数学试卷 题型:解答题
如图,二次函数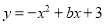 的图象与
的图象与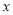 轴的一个交点为
轴的一个交点为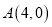 ,与
,与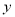 轴交于点
轴交于点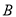 .
.
( )求此二次函数关系式和点
)求此二次函数关系式和点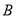 的坐标.
的坐标.
( )在
)在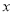 轴的正半轴上是否存在一点
轴的正半轴上是否存在一点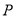 ,使得
,使得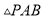 是以
是以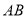 为底的等腰三角形?若存在,求出点
为底的等腰三角形?若存在,求出点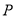 的坐标.若不存在,请说明理由.
的坐标.若不存在,请说明理由.
查看答案和解析>>
科目: 来源:2017-2018学年江苏省苏州市初三上期中模拟数学试卷 题型:解答题
已知关于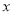 的方程:
的方程: 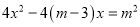 (
(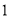 )求证:无论
)求证:无论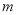 取什么实数值,这个方程总有两个相异实根.(
取什么实数值,这个方程总有两个相异实根.(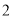 )若这个方程的两个实数根
)若这个方程的两个实数根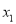 、
、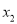 满足
满足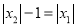 ,求
,求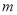 的值及相应的
的值及相应的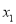 、
、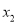 .
.
查看答案和解析>>
科目: 来源:2017-2018学年江苏省苏州市初三上期中模拟数学试卷 题型:解答题
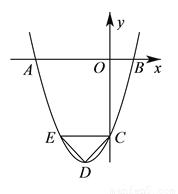
如图,抛物线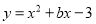 与
与 轴相交于
轴相交于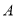 、
、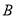 两点,与
两点,与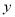 轴相交于点
轴相交于点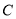 ,并且
,并且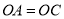 .
.
( )求这条抛物线的关系式;
)求这条抛物线的关系式;
(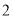 )过点
)过点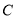 作
作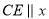 轴,交抛物线于点
轴,交抛物线于点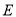 ,设抛物线的顶点为点
,设抛物线的顶点为点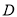 ,试判断
,试判断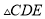 的形状,并说明理由.
的形状,并说明理由.
查看答案和解析>>
科目: 来源:2017-2018学年江苏省苏州市初三上期中模拟数学试卷 题型:解答题
如图,在一笔直的海岸线
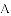
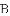
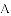
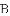
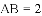
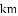
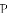
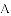
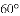
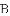
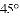
(1)求点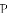

(2)小船从点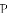
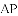
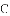
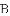
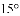
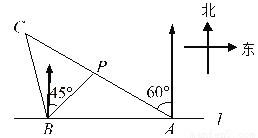
查看答案和解析>>
科目: 来源:2017-2018学年江苏省苏州市初三上期中模拟数学试卷 题型:解答题
某博物馆每周都吸引大量中外游客前来参观,如果游客过多,对馆中的珍贵文物会产生不利影响,但同时考虑到文物的修缮和保存费用问题,还要保证一定的门票收入,因此,博物馆采取了涨浮门票价格的方法来控制参观人数,在该方法实施过程中发现:每周参观人数与票价之间存在着如图所示的一次函数关系.在这种情况下,如果要保证每周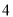 万元的门票收入,那么每周应限定参观人数是多少?门票价格应是多少.
万元的门票收入,那么每周应限定参观人数是多少?门票价格应是多少.
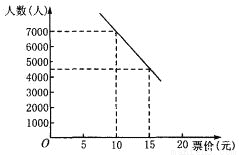
查看答案和解析>>
科目: 来源:2017-2018学年江苏省苏州市初三上期中模拟数学试卷 题型:解答题
如图,抛物线与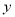 轴交于点
轴交于点 ,与
,与 轴交于
轴交于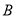 、
、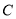 两点,其中
两点,其中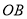 、
、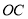 是方程的
是方程的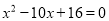 两根,且
两根,且 .
.
(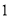 )求抛物线的解析式;
)求抛物线的解析式;
(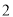 )直线
)直线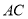 上是否存在点
上是否存在点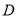 ,使
,使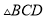 为直角三角形.若存在,求所有
为直角三角形.若存在,求所有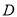 点坐标;反之说理;
点坐标;反之说理;
(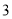 )点
)点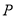 为
为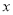 轴上方的抛物线上的一个动点(
轴上方的抛物线上的一个动点(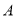 点除外),连
点除外),连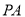 、
、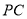 ,若设
,若设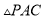 的面积为
的面积为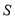 .
. 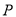 点横坐标为
点横坐标为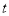 ,则
,则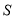 在何范围内时,相应的点
在何范围内时,相应的点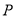 有且只有
有且只有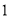 个.
个.
查看答案和解析>>
科目: 来源:黑龙江省2017-2018学年八年级数学上学期期末试卷 题型:单选题
如图,从下列四个条件:①BC=B′C;②AC=A′C;③∠A′CA=∠B′CB;④AB=A′B′中,任取三个为条件,余下的一个为结论,则最多可以构成正确的结论的个数是( )
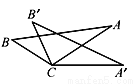
A. 1 B. 2
C. 3 D. 4
B 【解析】试题解析:当①②③为条件,④为结论时: ∵∠A′CA=∠B′CB, ∴∠A′CB′=∠ACB, ∵BC=B′C,AC=A′C, ∴△A′CB′≌△ACB, ∴AB=A′B′, 当①②④为条件,③为结论时: ∵BC=B′C,AC=A′C,AB=A′B′, ∴△A′CB′≌△ACB, ∴∠A′CB′=∠ACB, ∴∠A′CA=∠B′CB. 故选B.查看答案和解析>>
科目: 来源:黑龙江省2017-2018学年八年级数学上学期期末试卷 题型:单选题
如图,点P是∠AOB外的一点,点M,N分别是∠AOB两边上的点,点P关于OA的对称点Q恰好落在线段MN上,点P关于OB的对称点R落在MN的延长线上.若PM=2.5cm,PN=3cm,MN=4cm,则线段QR的长为( )
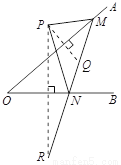
A. 4.5cm B. 5.5cm C. 6.5cm D. 7cm
A 【解析】试题分析:利用轴对称图形的性质得出PM=MQ,PN=NR,进而利用PM=2.5cm,PN=3cm,MN=4cm,得出NQ=MN-MQ=4-2.5=1.5(cm),即可得出QR的长RN+NQ=3+1.5=4.5(cm). 故选:A.查看答案和解析>>
科目: 来源:黑龙江省2017-2018学年八年级数学上学期期末试卷 题型:单选题
如图,∠A=15°,AB=BC=CD=DE=EF,则∠DEF等于( )
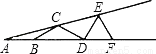
A.90° B.75° C.70° D.60°
D 【解析】 试题分析:根据已知条件,利用等腰三角形的性质及三角形的内角和外角之间的关系进行计算. 【解析】 ∵AB=BC=CD=DE=EF,∠A=15°, ∴∠BCA=∠A=15°, ∴∠CBD=∠BDC=∠BCA+∠A=15°+15°=30°, ∴∠BCD=180°﹣(∠CBD+∠BDC)=180°﹣60°=120°, ∴∠ECD=∠CED=180°...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com