练习册

  • 练习册
  • 试题
    相关习题
     0  320300  320308  320314  320318  320324  320326  320330  320336  320338  320344  320350  320354  320356  320360  320366  320368  320374  320378  320380  320384  320386  320390  320392  320394  320395  320396  320398  320399  320400  320402  320404  320408  320410  320414  320416  320420  320426  320428  320434  320438  320440  320444  320450  320456  320458  320464  320468  320470  320476  320480  320486  320494  366461 

    科目： 来源：2017-2018学年内蒙古乌兰察布市分校九年级（上）期中数学试卷 题型：填空题

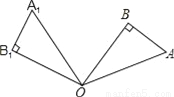
    如图，在直角△OAB中，∠AOB=30°，将△OAB绕点O逆时针旋转100°得到△OA1B1，则∠A1OB=______°．

    70 【解析】试题分析：根据旋转的性质可知，∠A1OA=100°，因为∠AOB=30°，所以∠A1OB=100°-30°=70°． 故答案为：70．

    查看答案和解析>>

    科目： 来源：2017-2018学年内蒙古乌兰察布市分校九年级（上）期中数学试卷 题型：填空题

    将二次函数y=x2﹣4x+5化成y=（x﹣h）2+k的形式，则y= ．

    y=（x﹣2）2+1． 【解析】y=x2-4x+5=x2-4x+4+1=(x-2)2+1.

    查看答案和解析>>

    科目： 来源：2017-2018学年内蒙古乌兰察布市分校九年级（上）期中数学试卷 题型：解答题

    已知：⊙O的半径为25cm，弦AB=40cm，弦CD=48cm，AB∥CD．求这两条平行弦AB，CD之间的距离______________．

    8cm或22cm 【解析】（1）如图1，连接OB，OD，做OM⊥AB交CD于点N， ∵AB∥CD， ∴ON⊥CD， ∵AB=40cm，CD=48cm， ∴BM=20cm，DN=24cm， ∵⊙O的半径为25cm， ∴OB=OD=25cm， ∴OM=15cm，ON=7cm， ∵MN=OM-ON， ∴MN=8cm， （2）如图2，连接OB，OD，做直线OM⊥AB交CD于点...

    查看答案和解析>>

    科目： 来源：2017-2018学年内蒙古乌兰察布市分校九年级（上）期中数学试卷 题型：填空题

    求经过A（1，4），B（﹣2，1）两点，对称轴为x=﹣1的抛物线的解析式_____．

    y=x2+2x+1 【解析】设抛物线解析式为y=ax2+bx+c， 根据题意得： , 解得：a=1，b=2，c=1， 则抛物线解析式为y=x2+2x+1． 故答案是：y=x2+2x+1.

    查看答案和解析>>

    科目： 来源：2017-2018学年内蒙古乌兰察布市分校九年级（上）期中数学试卷 题型：填空题

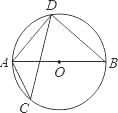
    如图，AB为⊙O直径，CD为⊙O的弦，∠ACD=25°，∠BAD的度数为 ．

    65°． 【解析】试题分析：根据直径所对的圆周角是直角，构造直角三角形ABD，再根据同弧所对的圆周角相等，求得∠B的度数，即可求得∠BAD的度数． ∵AB为⊙O直径 ∴∠ADB=90° ∵相同的弧所对应的圆周角相等，且∠ACD=25° ∴∠B=25° ∴∠BAD=90°﹣∠B=65°．

    查看答案和解析>>

    科目： 来源：2017-2018学年内蒙古乌兰察布市分校九年级（上）期中数学试卷 题型：填空题

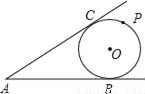
    如图所示，AB，AC与⊙O相切于点B，C，∠A=50°，点P是圆上异于B，C的一动点，则∠BPC的度数是_____．

    65°或115° 【解析】本题要分两种情况套，如下图，分别连接OC；OB；BP1；BP2；CP1；CP2 （1）当∠BPC为锐角，也就是∠BP1C时： ∵AB，AC与⊙O相切于点B，C两点 ∴OC⊥AC，OB⊥AB， ∴∠ACO=∠ABO=90°， ∵∠A=50°， ∴在四边形ABOC中，∠COB=130°， ∴∠BP1C=65°， （2）如果...

    查看答案和解析>>

    科目： 来源：2017-2018学年内蒙古乌兰察布市分校九年级（上）期中数学试卷 题型：填空题

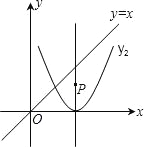
    如图，P是抛物线y=2（x﹣2）2对称轴上的一个动点，直线x=t平行y轴，分别与y=x、抛物线交于点A、B．若△ABP是以点A或点B为直角顶点的等腰直角三角形，求满足条件的t的值，则t= ．

    或1或3 【解析】 试题分析：依题意，y=2x2﹣8x+8，设A（t，t），B（t，2t2﹣8t+8），则AB=|t﹣（2t2﹣8t+8）|=|2t2﹣9t+8|，当△ABP是以点A为直角顶点的等腰直角三角形时，则∠PAB=90°，PA=AB=|t﹣2|；当△ABP是以点B为直角顶点的等腰直角三角形时，则∠PBA=90°，PB=AB=|t﹣2|；分别列方程求k的值． 试题解析：∵...

    查看答案和解析>>

    科目： 来源：2017-2018学年内蒙古乌兰察布市分校九年级（上）期中数学试卷 题型：解答题

    已知抛物线的顶点为（1，﹣4），且过点（﹣2，5）．

    （1）求抛物线解析式；

    （2）直接写出当函数值y＞0时，自变量x的取值范围．

    （1）y=（x﹣1）2﹣4；（2）x＜﹣1或x＞3． 【解析】试题分析： （1）由已知可设抛物线解析式为： ，代入点（-2，5）即可解得的值，从而可求得抛物线的解析式； （2）在（1）中所得抛物线的解析式中，由可得一元二次方程，解方程即可求得对应的的值，结合抛物线的开口方向，即可求得时，自变量的取值范围. 试题解析： （1）由已知可设抛物线解析式为： ， 把点（...

    查看答案和解析>>

    科目： 来源：2017-2018学年内蒙古乌兰察布市分校九年级（上）期中数学试卷 题型：解答题

    小李想用篱笆围成一个周长为60米的矩形场地，矩形面积S（单位：平方米）随矩形一边长x（单位：米）的变化而变化．

    （1）求S与x之间的函数关系式，并写出自变量x的取值范围；

    （2）当x是多少时，矩形场地面积S最大，最大面积是多少？

    (1)、S=x（30﹣x）(0＜x＜30)；(2)、x=15时，S有最大值为225平方米. 【解析】试题分析：(1)、已知周长为60米，一边长为x，则另一边长为30﹣x．(2)、用配方法化简函数解析式，求出s的最大值． 试题解析：(1)、S=x（30﹣x） 自变量x的取值范围为： 0＜x＜30． (2)、S=x（30﹣x） =﹣（x﹣15）2+225， ∴当x=15时，S有最大值...

    查看答案和解析>>

    科目： 来源：2017-2018学年内蒙古乌兰察布市分校九年级（上）期中数学试卷 题型：解答题

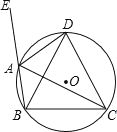
    如图，四边形ABCD内接于⊙O，∠DAE是四边形ABCD的一个外角，且AD平分∠CAE．

    求证：DB=DC．

    证明见解析． 【解析】试题分析：先根据圆周角定理得出∠DAC=∠DBC，再由角平分线的性质得出∠EAD=∠DAC，根据圆内接四边形的性质得出∠EAD=∠BCD，由此可得出结论． 试题解析：∵∠DAC与∠DBC是同弧所对的圆周角， ∴∠DAC=∠DBC． ∵AD平分∠CAE， ∴∠EAD=∠DAC， ∴∠EAD=∠DBC． ∵四边形ABCD内接于⊙O， ∴∠EAD=∠BCD， ...

    查看答案和解析>>

    同步练习册答案