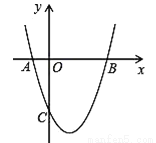
如图，抛物线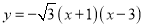与x轴交于A、B两点，与y轴交于点C，点D为该抛物线的对称轴上一点，当点D到直线BC和到x轴的距离相等时，则点D的坐标为 ．

或 【解析】试题分析：如图所示： ∵抛物线y=﹣（x+1）（x﹣3）与x轴交于A、B两点，与y轴交于点C， ∴当﹣（x+1）（x﹣3）=0时，x=﹣1，或x=3， 当x=0时，y=3， ∴A（﹣1，0），B（3，0），C（0，3），对称轴x=1， ∴BM=3﹣1=2， 当点D到直线BC和到x轴的距离相等时，点D在∠ABC或∠ABE的平分线上， ①点D...

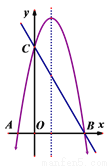
(1)计算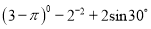： ； (2) 解方程：x2+4x+3=0．

（1）；（2）， 【解析】试题分析： （1）代入30°角的正弦函数值，结合“0指数幂的意义”和“负指数幂的意义”计算即可； （2）根据方程的特点，用“因式分解法”解答即可. 试题解析： （1）原式= = =. （2）原方程可化为： ， ∴或， 解得： .

近几年来，国家对购买新能源汽车实行补助政策，2017年某省对新能源汽车中的“插电式混合动力汽车”（用D表示）实行每辆3万元的补助，小刘对该省2017年上半年“纯电动乘用车”（有三种类型分别用A、B、C表示）和“插电式混合动力汽车”的销售计划进行了研究，绘制出如图所示的两幅不完整的统计图．

（1）补全条形统计图；

（2）求出“D”所在扇形的圆心角的度数；

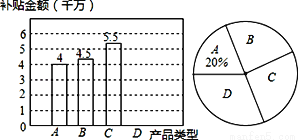
（3）为进一步落实该政策，该省计划再补助4.5千万元用于推广上述两大类产品，请你预测，该省16年计划大约共销售“插电式混合动力汽车”多少辆？

（1）补全条形图见解析；（2）108°；（3）预测该省16年计划大约共销售“插电式混合动力汽车”2450辆． 【解析】试题分析：（1）首先由A的数目和其所占的百分比可求出总数，进而可求出D的数目，问题得解；（2）由D的数目先求出它所占的百分比，再用百分比乘以360°，即可解答；（3）计算出补贴D类产品的总金额，再除以每辆车的补助可得车的数量． 试题解析：（1）补贴总金额为：4÷20%=...

小明、小刚和小红打算各自随机选择本周日的上午或下午去兴化李中水上森林游玩．

(1)小明和小刚都在本周日上午去游玩的概率为 ；

(2)求他们三人在同一个半天去游玩的概率．

（1）0.25；（2）. 【解析】（1）根据题意，画树状图列出三人随机选择上午或下午去游玩的所有等可能结果，找到小明和小刚都在本周日上午去游玩的结果，根据概率公式计算可得； （2）由（1）中树状图，找到三人在同一个半天去游玩的结果，根据概率公式计算可得． 【解析】 （1）根据题意，画树状图如图， 由树状图可知，三人随机选择本周日的上午或下午去游玩共有8种等可能结果， ...

如图，AB和DE是直立在地面上的两根立柱．AB=4 m，某一时刻AB在阳光下的投影BC=3 m．

(1)请你在图中画出此时DE在阳光下的投影．

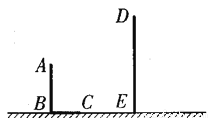
(2)在测量AB的投影时，同时测量出DE在阳光下的投影长为8 m，请你计算DE的长．

(1)详见解析；(2)DE=m. 【解析】试题分析：（1）根据投影的定义，作出投影即可； （2）根据在同一时刻，不同物体的物高和影长成比例；构造比例关系AB：DE=BC：EF．计算可得DE=10（m）． 试题解析：（1）连接AC，过点D作DF∥AC，交直线BC于点F，线段EF即为DE的投影． （2）∵AC∥DF， ∴∠ACB=∠DFE． ∵∠ABC=∠DEF=9...

如图，点E是矩形ABCD中CD边上一点，△BCE沿BE折叠为△BFE, 点F落在AD上.

(1)求证：△ABF∽△DFE；

(2)如果AB=12, BC=15, 求tan∠FBE的值；

（1）详见解析；（2）tan∠FBE=. 【解析】试题分析：（1）由矩形的性质推知∠A=∠D=∠C=90°．然后根据折叠的性质，等角的余角相等推知∠ABF=∠DFE，易证得△ABE∽△DFE； （2）由勾股定理求得AF=9，得出DF=6，由△ABF∽△DFE，求得EF=7.5，由三角函数定义即可得出结果． 试题解析：（1）∵四边形ABCD是矩形． ∴∠A=∠D=∠C=90°...

如图，抛物线y=x2 +bx+c与x轴交于A（﹣1，0），B（3，0）两点．

（1）求该抛物线的解析式；

（2）求该抛物线的对称轴以及顶点坐标；

（3）设（1）中的抛物线上有一个动点P，当点P在该抛物线上滑动到什么位置时，满足S△PAB=8，并求出此时P点的坐标．

（1）y=x2﹣2x﹣3；（2）抛物线的对称轴x=1，顶点坐标（1，﹣4）；（3）（，4）或（，4）或（1，﹣4）． 【解析】试题分析：（1）由于抛物线y=x2+bx+c与x轴交于A（﹣1，0），B（3，0）两点，那么可以得到方程x2+bx+c=0的两根为x=﹣1或x=3，然后利用根与系数即可确定b、c的值． （2）根据S△PAB=8，求得P的纵坐标，把纵坐标代入抛物线的解析式即可求得...

为给人们的生活带来方便，2017年兴化市准备在部分城区实施公共自行车免费服务．图1是公共自行车的实物图，图2是公共自行车的车架示意图，点A、D、C、E在同一条直线上，CD＝35cm，DF＝24cm，AF＝30cm，FD⊥AE于点D，座杆CE＝15cm，且∠EAB＝75°．

(1)求AD的长；

(2)求点E到AB的距离（结果保留整数）．

（参考数据：sin75°≈0.97，cos75°≈0.26，tan75°≈3.73）

图 1 图2

（1）AD=18;（2）车座点E到车架档AB的距离约是66cm． 【解析】（1）在Rt△ADF中，利用勾股定理可求出AD的长；（2）先考虑作辅助线，过点E作EH⊥AB，垂足为H，利用∠EAH的正弦列式求EH的长即可． 【解析】 （1）在Rt△ADF中，AF=30，DF=24， 由勾股定理得：AD==18cm； （2）过点E作EH⊥AB，垂足为H， ∵AE=AD+DC...

已知，点O在线段AB上，AB=6，OC为射线，且∠BOC=45°。动P以每秒1个单位长度的速度从点O出发，沿射线OC做匀速运动. 设运动时间为t 秒.

(1)如图，若AO=2。

① 当 t =6秒时，则OP = ， ；

② 当△ABP与△PBO相似时，求t的值；

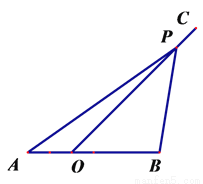
(2) 如图，若点O为线段AB的中点，当AP=AB时，过点A作AQ∥BP，并使得∠QOP=∠B，求AQ•BP的值。.

（1）6， ；（2）（+4）秒；（3）18． 【解析】试题分析：（1）①如图1中，作PE⊥AB于E．求出PE的长，根据S△APB=•AB•PE，即可计算． ②如图1中，过点B作OC的垂线，垂足为H，由△ABP∽△PBO，得，即PB2=BO•BA=24，推出BP=，再利用勾股定理求出OH、HP即可解决问题． （2）如图中，作OE∥AP，交BP于点E．由△QAO∽△OEP，得，即AQ...

已知在平面直角坐标系xOy中，O为坐标原点，线段AB的两个端点A（0，2），B（1，0）分别在y轴和x轴的正半轴上，点C为线段AB的中点，现将线段BA绕点B按顺时针方向旋转90°得到线段BD，抛物线y=ax2+bx+c（a≠0）经过点D．

（1）如图1，若该抛物线经过原点O，且．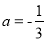

①求点D的坐标及该抛物线的解析式；

②连结CD，问：在抛物线上是否存在点P，使得∠POB与∠BCD互余？若存在，请求出所有满足条件的点P的坐标，若不存在，请说明理由；

（2）如图2，若该抛物线y=ax2+bx+c（a≠0）经过点E（1，1），点Q在抛物线上，且满足∠QOB与∠BCD互余．若符合条件的Q点的个数是3个，请直接写出a的值．

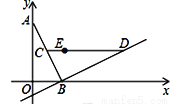
备用图

（1）①D的坐标是（3，1），y=﹣x2+x；②点P（， ）或（，﹣）；（2）a的值为a=． 【解析】试题分析： （1）①过点D作DF⊥x轴于点F，先通过三角形全等求得D的坐标，把D的坐标和a=﹣，c=0代入y=ax2+bx+c即可求得抛物线的解析式；②先证得CD∥x轴，进而求得要使得∠POB与∠BCD互余，则必须∠POB=∠BAO，设P的坐标为（x，﹣x2+x），分两种情况讨论即可求得；（...