
科目: 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷 题型:填空题
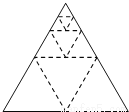
将一个正三角形纸片剪成四个全等的小正三角形,再将其中的一个按同样的方法剪成四个更小的正三角形,…如此继续下去,结果如下表.则an= .(用含n的代数式表示)
所剪次数 | 1 | 2 | 3 | 4 | … | n |
正三角形个数 | 4 | 7 | 10 | 13 | … | an |
查看答案和解析>>
科目: 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷 题型:解答题
先化简,再求值(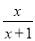 ﹣1)÷
﹣1)÷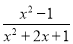 ,其中x=2sin60°+1.
,其中x=2sin60°+1.
查看答案和解析>>
科目: 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷 题型:解答题
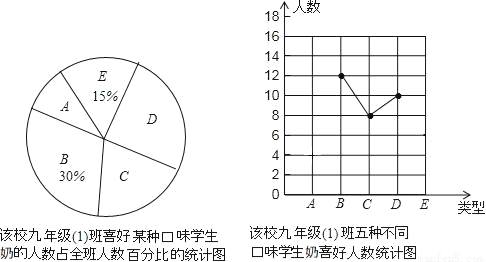
为了贯彻落实国家关于增强青少年体质的计划,我市全面实施了义务教育学段中小学学生“饮用奶计划”的营养工程.某牛奶供应商拟提供A(原味)、B(草莓味)、C(核桃味)、D(菠萝味)、E(香橙味)等五种口味的学生奶供学生选择(所有学生奶盒形状、大小相同),为了解对学生奶口味的喜好情况,某初级中学九年级(1)班张老师对全班同学进行了调查统计,制成了如图所示的两幅不完整的统计图.
(1)该班共有多少人?
(2)求出喜好A和E学生奶口味的人数;
(3)该班五种口味的学生奶喜好人数组成一组统计数据,求出这组数据的平均数;
(4)将折线统计图补充完整.
查看答案和解析>>
科目: 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷 题型:解答题
甲、乙、丙、丁四名同学进行一次乒乓球单打比赛,要从中选两位同学打第一场比赛.
(1)请用树状图或列表法求恰好选中甲、乙两位同学的概率;
(2)请利用若干个除颜色外其余都相同的乒乓球,设计一个摸球的实验(至少摸两次),
并根据该实验写出一个发生概率与(1)所求概率相同的事件.
(1)列表见解析,恰好选中甲、乙两位同学的概率为; (2)设计的方案见解析. 【解析】试题分析:(1)此题需要两步完成,所以采用树状图法或者采用列表法都比较简单,求得全部情况的总数与符合条件的情况数目;二者的比值就是其发生的概率;(2)根据题意设计合理的方法即可. 试题解析:(1)从中选出两位同学打第一场比赛所有可能出现的结果有: 共有12种,它们出现的可能性相同.所有的结...查看答案和解析>>
科目: 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷 题型:解答题
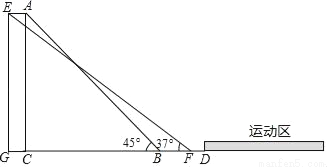
某学校为增加体育馆观众坐席数量,决定对体育馆进行施工改造.如图,为体育馆改造的截面示意图.已知原座位区最高点A到地面的铅直高度AC长度为15米,原坡面AB的倾斜角∠ABC为45°,原坡脚B与场馆中央的运动区边界的安全距离BD为5米.如果按照施工方提供的设计方案施工,新座位区最高点E到地面的铅直高度EG长度保持15米不变,使A、E两点间距离为2米,使改造后坡面EF的倾斜角∠EFG为37°.若学校要求新坡脚F需与场馆中央的运动区边界的安全距离FD至少保持2.5米(即FD≥2.5),请问施工方提供的设计方案是否满足安全要求呢?请说明理由.(参考数据:sin37°≈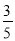 ,tan37°≈
,tan37°≈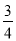 )
)
查看答案和解析>>
科目: 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷 题型:解答题
如图:已知AB是⊙O的直径,BC是⊙O的切线,OC与⊙O相交于点D,连结AD并延长,与BC相交于点E。
(1)若BC=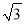 ,CD=1,求⊙O的半径;
,CD=1,求⊙O的半径;
(2)取BE的中点F,连结DF,求证:DF是⊙O的切线。

查看答案和解析>>
科目: 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷 题型:解答题
某饮料经营部每天的固定成本为200元,其销售的饮料每瓶进价为5元.销售单价与日平均销售的关系如下:
销售单价(元) | 6 | 6.5 | 7 | 7.5 | 8 | 8.5 | 9 |
日平均销售量(瓶) | 480 | 460 | 440 | 420 | 400 | 380 | 360 |
(1)若记销售单价比每瓶进价多x元,则销售量为_____(用含x的代数式表示);
求日均毛利润(日均毛利润=(每瓶售价-每瓶进价)×日均销售量-固定成本)y与x之间的函数关系式.
(2)若要使日均毛利润达到1400元,则销售单价应定为多少元?
(3)若要使日均毛利润达到最大,销售单价应定为多少元?最大日均毛利润为多少元?
(1)520﹣40x,y=﹣40x2+520x﹣200(0<x<13);(2)10元;(3)销售单价定为11.5元,日均毛利润达到最大值1490元. 【解析】试题分析: (1)观察表格中的数据可知,当销售价格每上涨0.5元时,销售量会减少20瓶,由此可得若记销售单价比每瓶进价多元,则销售量为: ,化简即可得所求答案;由日均毛利润=(每瓶售价-每瓶进价)×日均销售量-固定成本,列式即可得...查看答案和解析>>
科目: 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷 题型:解答题
在四边形ABCD中,对角线AC、BD相交于点O,设锐角∠AOB=α,将△DOC按逆时针方向旋转得到△D′OC′(0°<旋转角<90°)连接AC′、BD′,AC′与BD′相交于点M.
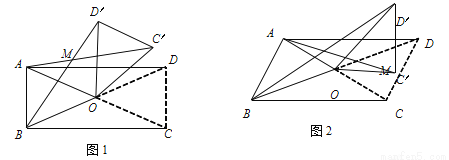
(1)、当四边形ABCD为矩形时,如图1.求证:△AOC′≌△BOD′.
(2)、当四边形ABCD为平行四边形时,设AC=kBD,如图2.
①猜想此时△AOC′与△BOD′有何关系,证明你的猜想;
②探究AC′与BD′的数量关系以及∠AMB与α的大小关系,并给予证明.
(1)见解析;(2)①、△BOD′∽△AOC′;(2)AC′=kBD′,∠AMB=α. 【解析】试题分析:(1)证明:在矩形ABCD中,AC=BD,OA=OC=AC,OB=OD=BD,∴OA=OC=OB=OD,又∵OD=OD′,OC=OC′,∴OB=OD′=OA=OC′,∵∠D′OD=∠C′OC,∴180°﹣∠D′OD=180°﹣∠C′OC,∴∠BOD′=∠AOC′,∴在△BOD′和△AOC...查看答案和解析>>
科目: 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷 题型:解答题
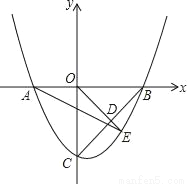
如图,对称轴为直线x=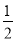 的抛物线与y轴交于点C(0,﹣3),与x轴交于A、B两点(点A在点B的左侧),AB=5
的抛物线与y轴交于点C(0,﹣3),与x轴交于A、B两点(点A在点B的左侧),AB=5
(1)求A、B两点的坐标及该抛物线对应的解析式;
(2)D为BC的中点,延长OD与抛物线在第四象限内交于点E,连结AE、BE.
①求点E的坐标;
②判断ABE的形状,并说明理由;
(3)在x轴下方的抛物线上,是否存在一点P,使得四边形OBEP是平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com