
科目: 来源:浙江省温州市瑞安市五校联考2018届九年级上学期期末学业检测数学试卷 题型:填空题
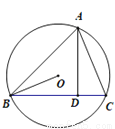
如图,△ABC内接于⊙O,AD⊥BC于点D,AD=BD.若⊙O的半径OB=2,则AC的长为____.
查看答案和解析>>
科目: 来源:浙江省温州市瑞安市五校联考2018届九年级上学期期末学业检测数学试卷 题型:填空题
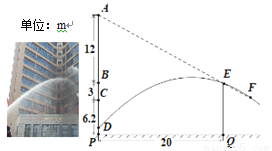
两幢大楼的部分截面及相关数据如图,小明在甲楼A处透过窗户E发现乙楼F处出现火灾,此时A,E,F在同一直线上.跑到一楼时,消防员正在进行喷水灭火,水流路线呈抛物线,在1.2m高的D处喷出,水流正好经过E,F. 若点B和点E、点C和F的离地高度分别相同,现消防员将水流抛物线向上平移0.4m,再向左后退了____m,恰好把水喷到F处进行灭火.
查看答案和解析>>
科目: 来源:浙江省温州市瑞安市五校联考2018届九年级上学期期末学业检测数学试卷 题型:解答题
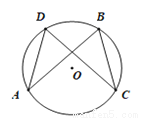
如图,在⊙O中,AB=CD.求证:AD=BC.
查看答案和解析>>
科目: 来源:浙江省温州市瑞安市五校联考2018届九年级上学期期末学业检测数学试卷 题型:解答题
一个不透明的袋子中装有红、白两种颜色的小球,这些球除颜色外都相同,其中红球有2个,若从中随机摸出一个球,这个球是白球的概率为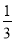 .
.
(1)求袋子中白球的个数;(请通过列式或列方程解答)
(2)随机摸出一个球后,放回并搅匀,再随机摸出一个球,求两次都摸到相同颜色的小球的概率.(请结合树状图或列表解答)
(1)1;(2). 【解析】试题分析:(1)首先设袋子中白球有x个,利用概率公式求得方程: ,解此方程即可求得答案; (2)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与两次都摸到相同颜色的小球的情况,再利用概率公式即可求得答案. 【解析】 (1)设白球有x个,则有,解得x=1(检验可不写) (2)树状图或列表3分,计算概率2分: 所以,两次都摸到相同颜...查看答案和解析>>
科目: 来源:浙江省温州市瑞安市五校联考2018届九年级上学期期末学业检测数学试卷 题型:解答题
如图,点O是线段AB的中点,根据要求完成下题:
(1)在图中补画完成:
第一步,以AB为直径的画出⊙O;
第二步,以B为圆心,以BO为半径画圆弧,交⊙O于点C,连接点CA,CO;
(2)设AB=6,求扇形AOC的面积.(结果保留π)
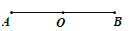
查看答案和解析>>
科目: 来源:浙江省温州市瑞安市五校联考2018届九年级上学期期末学业检测数学试卷 题型:解答题
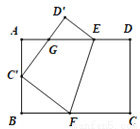
如图,将矩形ABCD沿EF折叠,使顶点C恰好落在AB边的C'处,点D落在点D'处,C'D'交线段AE于点G.
(1)求证:△BC'F∽△AGC';
(2)若C'是AB的中点,AB=6,BC=9,求AG的长.
查看答案和解析>>
科目: 来源:浙江省温州市瑞安市五校联考2018届九年级上学期期末学业检测数学试卷 题型:解答题
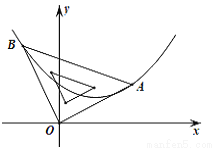
如图,二次函数的图象的顶点坐标为(1, 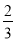 ),现将等腰直角三角板直角顶点放在原点O,一个锐角顶点A在此二次函数的图象上,而另一个锐角顶点B在第二象限,且点A的坐标为(2,1).
),现将等腰直角三角板直角顶点放在原点O,一个锐角顶点A在此二次函数的图象上,而另一个锐角顶点B在第二象限,且点A的坐标为(2,1).
(1)求该二次函数的表达式;
(2)判断点B是否在此二次函数的图象上,并说明理由.
查看答案和解析>>
科目: 来源:浙江省温州市瑞安市五校联考2018届九年级上学期期末学业检测数学试卷 题型:解答题
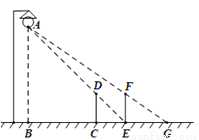
甲乙两位同学利用灯光下的影子来测量一路灯A的高度,如图,当甲走到点C处时,乙测得甲直立身高CD与其影子长CE正好相等,接着甲沿BC方向继续向前走,走到点E处时,甲直立身高EF的影子恰好是线段EG,并测得EG=2.5m.已知甲直立时的身高为1.75m,求路灯的高AB的长.(结果精确到0.1m)
查看答案和解析>>
科目: 来源:浙江省温州市瑞安市五校联考2018届九年级上学期期末学业检测数学试卷 题型:解答题
如图,二次函数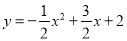 的图象与x轴交于点A,B,与y轴交于点C.点P是该函数图象上的动点,且位于第一象限,设点P的横坐标为x.
的图象与x轴交于点A,B,与y轴交于点C.点P是该函数图象上的动点,且位于第一象限,设点P的横坐标为x.
(1)写出线段AC, BC的长度:AC= ,BC= ;
(2)记△BCP的面积为S,求S关于x的函数表达式;
(3)过点P作PH⊥BC,垂足为H,连结AH,AP,设AP与BC交于点K,探究:是否存在四边形ACPH为平行四边形?若存在,请求出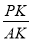 的值;若不存在,请说明理由,并求出
的值;若不存在,请说明理由,并求出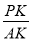 的最大值.
的最大值.
查看答案和解析>>
科目: 来源:浙江省温州市瑞安市五校联考2018届九年级上学期期末学业检测数学试卷 题型:解答题
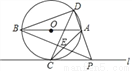
如图,AB是⊙O的直径,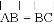 ,连结AC,过点C作直线l∥AB,点P是直线l上的一个动点,直线PA与⊙O交于另一点D,连结CD,设直线PB与直线AC交于点E.
,连结AC,过点C作直线l∥AB,点P是直线l上的一个动点,直线PA与⊙O交于另一点D,连结CD,设直线PB与直线AC交于点E.
(1)求∠BAC的度数;
(2)当点D在AB上方,且CD⊥BP时,求证:PC=AC;
(3)在点P的运动过程中
①当点A在线段PB的中垂线上或点B在线段PA的中垂线上时,求出所有满足条件的∠ACD的度数;
②设⊙O的半径为6,点E到直线l的距离为3,连结BD,DE,直接写出△BDE的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com