已知抛物线y=x2﹣2mx+m2﹣1（m是常数）的顶点为P，直线l：y=x﹣1．

（1）求证：点P在直线l上．

（2）若抛物线的对称轴为x=﹣3，直接写出该抛物线的顶点坐标　 　，与x轴交点坐标为　 　．

（3）在（2）条件下，抛物线上点（﹣2，b）在图象上的对称点的坐标是　 　．

（﹣4，﹣3） 【解析】试题分析：（1）利用配方法得到y=（x﹣m）2+m﹣1，点P（m，m﹣1），然后根据一次函数图象上点的坐标特征判断点P在直线l上； （2）由（1）可知抛物线的对称轴为x=m，结合已知条件则可得m=﹣3，进而可求出抛物线的顶点坐标；设y=0，则x轴交点坐标也可求出； （3）把点（﹣2，b）代入抛物线解析式可求出b的值，进而可求出在图象上的对称点的坐标． ...

如图，二次函数y=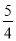x2（0≤x≤2）的图象记为曲线C1，将C1绕坐标原点O逆时针旋转90°，得曲线C2

（1）请画出C2；

（2）写出旋转后A（2，5）的对应点A1的坐标；

（3）直接写出C1旋转至C2过程中扫过的面积．

（1）见解析；（2）A1（﹣5，2）．（3）． 【解析】试题分析：（1）根据图形旋转的性质画出曲线C2即可； （2）根据点A1在坐标系中的位置即可得出结论； （3）先求出OA的长，再由扇形的面积公式即可得出结论． 试题解析：（1）如图，曲线C2即为所求； （2）由图可知，A1（﹣5，2）． （3）∵OA=， ∴C1旋转至C2过程中扫过的面积= ． ...

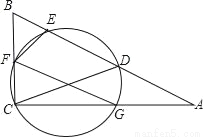
如图，D为Rt△ABC斜边AB上一点，以CD为直径的圆分别交△ABC三边于E、F、G三点，连接FE，FG．

（1）求证：∠EFG=∠B；

（2）若AC=2BC=4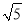，D为AE的中点，求FG的长．

（1）证明见解析；（2）4 【解析】试题分析：（1）连接EC，则∠AEC=90°，由同角的余角相等即可得出∠B=∠ECA，再根据圆周角定理即可得出∠ECA=∠EFG，由此即可证出∠EFG=∠B； （2）由AC、BC的长度利用勾股定理即可求出AB的长度，结合面积法即可得出CE的长度，由正切即可得出AE的长度，再利用勾股定理可求出CD的长度，连接FD、DG，由矩形的判定定理即可证出四边形F...

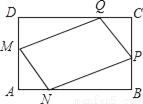
为了美化环境，学校准备在如图所示的矩形ABCD空地上进行绿化，规划在中间的一块四边形MNQP上种花，其余的四块三角形上铺设草坪，要求AM=AN=CP=CQ，已知BC=24米，AB=40米，设AN=x米，种花的面积为y1平方米，草坪面积y2平方米．

（1）分别求y1和y2与x之间的函数关系式（不要求写出自变量的取值范围）；

（2）当AN的长为多少米时，种花的面积为440平方米？

（3）若种花每平方米需200元，铺设草坪每平方米需100元，现设计要求种花的面积不大于440平方米，设学校所需费用W（元），求W与x之间的函数关系式，并求出学校所需费用的最大值．

（1）y2=2x2﹣64x+960，y1=﹣2x2+64x；（2）10米或22米； （3）W=﹣200（x﹣16）2+147200，最大值为140000元. 【解析】试题分析：（1）根据三角形面积公式可得y2的解析式，再用长方形面积减去四个三角形面积，即可得y1的函数解析式； （2）根据题意知y1=440，即即可得关于x的方程，解方程即可得； （3）列出总费用的函数解析式，...

如图，抛物线y=ax2+2ax+c的图象与x轴交于A、B两点（点A在点B的左边）AB=4，与y轴交于点C，OC=OA，点D为抛物线的顶点．

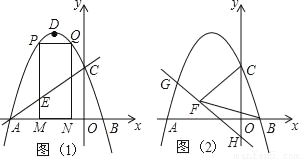
（1）求抛物线的解析式；

（2）点M（m，0）为线段AB上一点（点M不与点A、B重合），过点M作x轴的垂线，与直线AC交于点E，与抛物线交于点P，过点P作PQ∥AB交抛物线于点Q，过点Q作QN⊥x轴于点N，可得矩形PQNM，如图1，点P在点Q左边，当矩形PQNM的周长最大时，求m的值，并求出此时的△AEM的面积；

（3）已知H（0，﹣1），点G在抛物线上，连HG，直线HG⊥CF，垂足为F，若BF=BC，求点G的坐标．

（1）y=﹣x2﹣2x+3； （2）m=﹣2, ； （3）点G的坐标为（， ）或（， ）． 【解析】试题分析：（1）根据抛物线y=ax2+2ax+c，可得C（0，c），对称轴为x﹣1，再根据OC=OA，AB=4，可得A（﹣3，0），最后代入抛物线y=ax2+2ax+3，得抛物线的解析式为y=﹣x2﹣2x+3； （2）根据点M（m，0），可得矩形PQNM中，P（m，﹣m2﹣2m+3...

下列图形中可由其中的部分图形经过平移得到的是(　 　)

A. A B. B C. C D. D

A 【解析】试题解析：平移前后，两图形的大小不变，形状不变，对应点连成的线段平行且相等. 可知A符合平移的特征. 故选A.

已知二元一次方程3x－y=1，当x=2时，y等于（ ）

A．5 B．－3 C．－7 D．7

A 【解析】 试题分析：先根据解的定义，把x=2代入方程中可得到关于y的方程，解之即可．

将不等式2(x＋1)－1≥3x的解集表示在数轴上，正确的是(　 　)

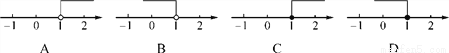
A. A B. B C. C D. D

D 【解析】试题解析：去括号，得： 移项，得： 合并同类项，得： 系数化为1，得： 故选D.

如图，在铁路旁有一李庄O，现要建一火车站，为了使李庄人乘车最方便，请你在铁路线上选一点来建火车站，应建在(　 　)

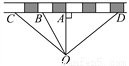
A. A点 B. B点 C. C点 D. D点

A 【解析】试题解析：根据垂线段最短可得：应建在A处， 故选A.

代入法解方程组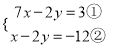有以下步骤：(1)由①，得2y＝7x－3③；(2)把③代入①，得7x－7x－3＝3；(3)整理，得3＝3；(4)∴x可取一切有理数，原方程组有无数组解．以上解法造成错误步骤是(　 　)

A. 第(1)步 B. 第(2)步 C. 第(3)步 D. 第(4)步

B 【解析】试题解析：错的是第步，应该将③代入②. 故选B.