相关习题
0 320534 320542 320548 320552 320558 320560 320564 320570 320572 320578 320584 320588 320590 320594 320600 320602 320608 320612 320614 320618 320620 320624 320626 320628 320629 320630 320632 320633 320634 320636 320638 320642 320644 320648 320650 320654 320660 320662 320668 320672 320674 320678 320684 320690 320692 320698 320702 320704 320710 320714 320720 320728 366461
科目:
来源:2017-2018学年八年级数学下册(北师大版):期中检测题
题型:填空题
如图,在Rt△ABC中,∠C=90°,AC=4,将△ABC沿CB方向平移得到△DEF,若四边形ABED的面积等于8,则平移的距离为_____.
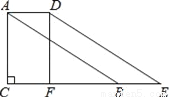
2
【解析】∵将△ABC沿CB向右平移得到△DEF,四边形ABED的面积等于8,AC=4,
∴平移距离=8÷4=2.
查看答案和解析>>
科目:
来源:2017-2018学年八年级数学下册(北师大版):期中检测题
题型:填空题
如图,在△ABC中,BI,CI分别平分∠ABC,∠ACF,直线DE过点I,且DE∥BC,BD=8 cm,CE=5 cm,则DE=______.
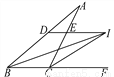
3cm
【解析】【解析】
∵BI、CI分别平分∠ABC、∠ACF,∴∠ABI=∠CBI,∠ECI=∠ICF.∵DE∥BC,∴∠DIB=∠CBI,∠EIC=∠ICF,∴∠ABI=∠DIB,∠ECI=∠EIC,∴DI=BD=8cm,EI=CE=5cm,∴DE=DI﹣EI=3(cm).故答案为:3cm.
查看答案和解析>>
科目:
来源:2017-2018学年八年级数学下册(北师大版):期中检测题
题型:填空题
如图,OA⊥OB,Rt△CDE的边CD在OB上,∠ECD=45°,CE=4,若将△CDE绕点C逆时针旋转75°,点E的对应点N恰好落在OA上,则OC的长度为______.

2
【解析】【解析】
∵将三角形CDE绕点C逆时针旋转75°,点E的对应点N恰好落在OA上,∴∠ECN=75°.∵∠ECD=45°,∴∠NCO=180°﹣75°﹣45°=60°.∵AO⊥OB,∴∠AOB=90°,∴∠ONC=30°.∵CE=4,∴CN=4,∴OC=2.故答案为:2.
查看答案和解析>>
科目:
来源:2017-2018学年八年级数学下册(北师大版):期中检测题
题型:填空题
如图,把等边△A BC沿着D E折叠,使点A恰好落在BC边上的点P处,且DP⊥BC,若BP=4cm,则EC=______cm.
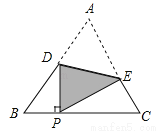
【解析】∵△ABC是等边三角形,∴∠A=∠B=∠C=60°,AB=BC,
∵DP⊥BC,∴∠BPD=90°,
∵PB=4cm,∴BD=8cm,PD=cm,
∵把等边△A BC沿着D E折叠,使点A恰好落在BC边上的点P处,
∴AD=PD=cm,∠DPE=∠A=60°,∴AB=(8+)cm,
∴BC=(8+)cm,∴PC=BC﹣BP=(4+)cm,
∵∠EPC=1...
查看答案和解析>>
科目:
来源:2017-2018学年八年级数学下册(北师大版):期中检测题
题型:填空题
如图,△ABC的外角∠ACD的平分线CP与内角∠ABC平分线BP交于点P,若∠BPC=40°,则∠CAP= .
50°
【解析】
试题分析:根据外角与内角性质得出∠BAC的度数,再利用角平分线的性质以及直角三角形全等的判定,得出∠CAP=∠FAP,即可得出答案.延长BA,作PN⊥BD,PF⊥BA,PM⊥AC, 设∠PCD=x°,
∵CP平分∠ACD, ∴∠ACP=∠PCD=x°,PM=PN, ∵BP平分∠ABC, ∴∠ABP=∠PBC,PF=PN,
∴PF=PM, ∵∠BPC=40°...
查看答案和解析>>
科目:
来源:2017-2018学年八年级数学下册(北师大版):期中检测题
题型:解答题
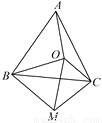
(1)解不等式: 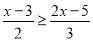 ,并写出它的正整数解;
,并写出它的正整数解;
(2)解不等式组
(1)x=1(2)无解
【解析】试题分析:(1)去分母,去括号,移项,合并同类项,系数化成1即可;
(2)分别求出不等式组中两不等式的解集,找出解集的公共部分即可确定出不等式组的解集.
试题解析:【解析】
(1)去分母得:3(x﹣3)≥2(2x﹣5),3x﹣9≥4x﹣10,3x﹣4x≥﹣10+9,﹣x≥﹣1,x≤1,所以不等式的正整数解为x=1;
(2),由①得:x≥1,...
查看答案和解析>>
科目:
来源:2017-2018学年八年级数学下册(北师大版):期中检测题
题型:解答题
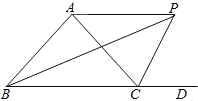
如图,在平面直角坐标系中,图形①,②关于点P中心对称.
(1)画出对称中心P,并写出点P的坐标;
(2)将图形②向下平移4个单位长度,画出平移后的图形③,并判断图形③与图形①的位置关系.(直接写出结果)

(1)点P的坐标为(1,5) (2)图形③与图形①关于点Q(1,3)中心对称
【解析】试题分析:(1)连接各对应点,线段的交点即是点P;
(2)根据平移的性质,把图形的各点向下平移4个单位后,得到新点,顺次连接画图即可,然后观察两图的关系.
试题解析:【解析】
(1)画点P, P(1,5);
(2)画图形③, 图形③与图形①关于点Q(1,3)成中心对称.
查看答案和解析>>
科目:
来源:2017-2018学年八年级数学下册(北师大版):期中检测题
题型:解答题
如图,点D,E在△ABC的边BC上,连 接AD,AE.①AB=AC;②AD=AE;③BD=CE.以此三个等式中的两个作为命题的题设,另一个作为命题的结论,构成三个命题:①②⇒③:①③⇒②;②③⇒①.
(1)以上三个命题是真命题的为(直接作答) ;
(2)请选择一个真命题进行证明(先写出所选命题,然后证明)

(1)①②⇒③,①③⇒②,②③⇒①; (2)选择①③⇒②,证明见解析.
【解析】
试题分析:(1)根据真命题的定义即可得出结论,
(2)根据全等三角形的判定方法及全等三角形的性质即可证明.
试题解析:(1)①②⇒③,①③⇒②,②③⇒①,
(2)选择①③⇒②,
证明:∵AB=AC,
∴∠B=∠C,
在△ABD和△ACE中,
∵
∴△ABD≌...
查看答案和解析>>
科目:
来源:2017-2018学年八年级数学下册(北师大版):期中检测题
题型:解答题
如图,在△ABC中,∠C=90°,DE垂直平分AB,交BC于点D,连接AD,若AC=8,DC:AD=3:5.求:
(1)CD的长;
(2)DE的长.
(1) 6(2)2
【解析】试题分析:(1)由在Rt△ACD中,DC:AD=3:5,设CD=3k,则AD=5k,利用方程思想与勾股定理即可求得CD的长;
(2)根据垂直平分线的性质,即可求得BD的值,则可得BC与AB的值,在Rt△BDE中,利用勾股定理求解即可.
试题解析:【解析】
(1)在Rt△ACD中,∠C=90°,DC:AD=3:5,设CD=3k,AD=5k,∴AC==4...
查看答案和解析>>
科目:
来源:2017-2018学年八年级数学下册(北师大版):期中检测题
题型:解答题
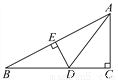
如图,点O为等边三角形ABC内一点,连接OA,OB,OC,以OB为一边作∠OBM=60°,且BO=BM,连接CM,OM.
(1)判断AO与CM的大小关系并证明;
(2)若OA=8,OC=6,OB=10,判断△OMC的形状并证明.
(1)AO=CM (2)△OMC是直角三角形
【解析】试题分析:(1)先证明△OBM是等边三角形,得出OM=OB,∠ABC=∠OBC,由SAS证明△AOB≌△CMB,即可得出结论;
(2)由勾股定理的逆定理即可得出结论.
试题解析:【解析】
(1)AO=CM.理由如下:
∵∠OBM=60°,OB=BM,∴△OBM是等边三角形,∴OM=OB=10,∠ABC=∠OBC=60°...
查看答案和解析>>






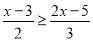 ,并写出它的正整数解;
,并写出它的正整数解;



