
科目: 来源:2018春季学北师大版九年级数学下册期末测评试卷 题型:单选题
如果一个扇形的弧长等于它的半径,那么此扇形称为“等边扇形”.则半径为2的“等边扇形”的面积为( )
A. π B. 1 C. 2 D. 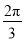
查看答案和解析>>
科目: 来源:2018春季学北师大版九年级数学下册期末测评试卷 题型:填空题
在△ABC中,sin B=cos(90°-C)= 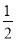 ,则△ABC的形状是________.
,则△ABC的形状是________.
查看答案和解析>>
科目: 来源:2018春季学北师大版九年级数学下册期末测评试卷 题型:填空题
如图,某登山运动员从营地A沿坡角为30°的斜坡AB到达山顶B,如果AB=2000米,则他实际上升了________米.
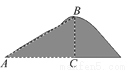
查看答案和解析>>
科目: 来源:2018春季学北师大版九年级数学下册期末测评试卷 题型:填空题
二次函数y=-x2+2x-3图象的顶点坐标是_____________________.
(-1,-4) 【解析】试题解析: 故顶点坐标为: 故答案为:查看答案和解析>>
科目: 来源:2018春季学北师大版九年级数学下册期末测评试卷 题型:填空题
△ABC中,AB=10 cm,AC=8 cm,BC=6 cm,以点B为圆心,6 cm为半径作☉B,则边AC所在的直线与☉B的位置关系是___.
相切 【解析】试题解析:∵△ABC中,AB=10cm,AC=8cm,BC=6cm, 则圆心到直线的距离即为BC的长6cm,等于圆的半径,则直线和圆相切. 故答案为:相切.查看答案和解析>>
科目: 来源:2018春季学北师大版九年级数学下册期末测评试卷 题型:填空题
如图,用12 m长的木条,做一个有一条横档的矩形窗子,为使透进的光线最多,选择窗子的高AB为___.
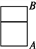
查看答案和解析>>
科目: 来源:2018春季学北师大版九年级数学下册期末测评试卷 题型:填空题
如图,☉O的直径AB=8,AC=3CB,过点C作AB的垂线交☉O于M,N两点,连接MB,则∠MBA的余弦值为_____.
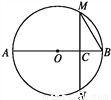
查看答案和解析>>
科目: 来源:2018春季学北师大版九年级数学下册期末测评试卷 题型:填空题
如图,已知点A从点(1,0)出发,以每秒1个单位长度的速度沿着x轴的正方向运动,经过t s后,以O,A为顶点作菱形OABC,使点B,C都在第一象限内,且∠AOC=60°,又以点P(0,4)为圆心,PC为半径的圆恰好与OA所在的直线相切,则t=_____.
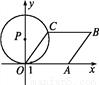
查看答案和解析>>
科目: 来源:2018春季学北师大版九年级数学下册期末测评试卷 题型:解答题
如图,有一长为4 cm,宽为3 cm的长方形木板在桌面上做无滑动的翻滚(顺时针方向),木板上的顶点A的位置变化为A→A1→A2,其中第二次翻滚被桌面上一小木块挡住,使木板边沿A2C与桌面成30°角,则点A翻滚到A2位置时,共走过的路径长为____.
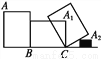
查看答案和解析>>
科目: 来源:2018春季学北师大版九年级数学下册期末测评试卷 题型:解答题
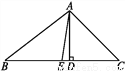
如图,在△ABC中,AD是BC边上的高,AE是BC边上的中线,∠C=45°,sin B=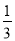 ,AD=1.
,AD=1.
求:(1)BC的长;
(2)tan∠DAE的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com