
科目: 来源:湖北省2017-2018学年九年级上期元月调考数学试卷(2) 题型:解答题
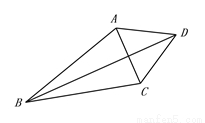
如图,在△ABC中,以AC为边在△ABC外作正△ACD,连接BD.
(1)以点A为中心,把△ADB顺时针旋转60°,画出旋转后的图形(保留作图痕迹);
(2)若∠ABC=30°,BC=4,BD=6,求AB的长.
查看答案和解析>>
科目: 来源:湖北省2017-2018学年九年级上期元月调考数学试卷(2) 题型:解答题
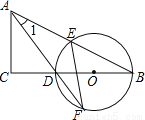
如图,在△ABC中,∠C= 90°,D是BC边上一点,以DB为直径的⊙O经过AB的中点E,交AD的延长线于点F,连接EF.
(1)求证:∠1= ∠F;
(2)若CD= 3,EF=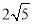 ,求⊙O的半径长.
,求⊙O的半径长.
查看答案和解析>>
科目: 来源:湖北省2017-2018学年九年级上期元月调考数学试卷(2) 题型:解答题
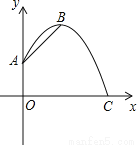
一自动喷灌设备的喷流情况如图所示,设水管OA在高出地面1.5米的A处有一自动旋转的喷水头,一瞬间流出的水流是抛物线状,喷头A与水流最高点B连线与y轴成45°角,水流最高点B比喷头A高2米.
(1)求水流落地点C到O点的距离;
(2)若水流的水平位移s(米)(抛物线上两对称点之间的距离)与水流的运动时间(t秒)之间的函数关系为t= 0.8s,求共有几秒钟,水流高度不低于2米?
查看答案和解析>>
科目: 来源:湖北省2017-2018学年九年级上期元月调考数学试卷(2) 题型:解答题
某工艺品每件的成本是50元,在某段时间内若以每件x元出售,可卖出(200-2x)件,设这段时间内售出该工艺品的利润为y元.
(1)直接写出利润y(元)与售价x(元)之间的函数关系式;
(2)求出销售单价为多少元时,每天的销售利润最大?最大利润是多少?
(3)如果要使利润不低于1200元,且成本不超过2500元,请直接写出x的范围为_____________.
(1)y=-2x2+300x-10000;(2)单价为75元时,最大利润为1250元;(3)75≤x≤80. 【解析】试题分析:(1)利用销量×每件利润进而得出y与x的函数关系式; (2)利用二次函数的性质进行进行求解即可; (3)根据利润不低于1200元,成本不超过2500元,列不等式组进行求解即可. 试题解析:(1)由题意可得:y=(x-50)(200-2x)=﹣2x2...查看答案和解析>>
科目: 来源:湖北省2017-2018学年九年级上期元月调考数学试卷(2) 题型:解答题
以C为直角顶点的两个等腰直角△CAB和△CDG,E为AB的中点,F为DG的中点.
(1)如图1,点A、B分别在边CD,CG上,则EF与AD的数量关系是______________;
(2)如图2,点A、B不在边CD、CG上,(1)中EF与AD的关系还成立吗?请证明你的结论;
(3)如图3,若A、B、G在同一直线上,且A、C、B、F在同一圆上,直接写出△CDG与△CAB面积之比.
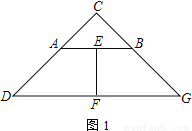
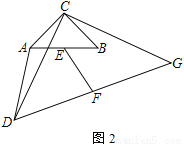
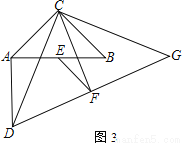
查看答案和解析>>
科目: 来源:湖北省2017-2018学年九年级上期元月调考数学试卷(2) 题型:解答题
如图1,已知抛物线y=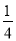 x2—1与x轴交于A、B两点,顶点为C.
x2—1与x轴交于A、B两点,顶点为C.
(1)求A,B两点的坐标;
(2)若点P为抛物线上的一点,且S△APC=2,求点P的坐标;
(3)如图2,P(﹣2,﹣2),直线BD交抛物线于D,交y轴于M,连DP交抛物线于E,连BE交y轴于N,求CM • ON的值.
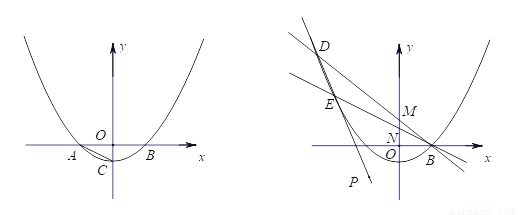
图1 图2
(1)A(﹣2,0),B(2,0);(2)P(﹣4,3)或P(2,0);(3)2. 【解析】试题分析:(1)令y=0,则有0=x2—1,解方程即可得; (2)在y轴正半轴上取一点M使S△ACM=2,则可得M(0,1),过M作AC的平行线与抛物线的交点即为满足条件的点; (3)根据已知设yDP=kx+2k-2,D(x1,y1),E(x2,y2),联立可得x1+x2=4k,x1·x2...查看答案和解析>>
科目: 来源:贵州省遵义市2018届九年级(上)第一次月考数学试卷 题型:单选题
抛物线y=2(x+3)2+1的顶点坐标是( )
A. (3,1) B. (3,﹣1) C. (﹣3,1) D. (﹣3,﹣1)
C 【解析】由函数y=a(x-h)2+k的顶点坐标为(h,k)可得抛物线y=2(x+3)2+1的顶点坐标是(-3,1),故选C.查看答案和解析>>
科目: 来源:贵州省遵义市2018届九年级(上)第一次月考数学试卷 题型:单选题
下列方程中,是关于x的一元二次方程的为( )
A. 2x2 = 0 B. 4x2=3y
C. x2+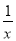 =﹣1 D. x2=(x﹣1)(x﹣2)
=﹣1 D. x2=(x﹣1)(x﹣2)
查看答案和解析>>
科目: 来源:贵州省遵义市2018届九年级(上)第一次月考数学试卷 题型:单选题
把抛物线y=(x+1)2向下平移2个单位,再向右平移1个单位,所得到的抛物线是( )
A. y=(x+2)2+2 B. y=(x+2)2﹣2 C. y=x2+2 D. y=x2﹣2
D 【解析】根据二次函数图象平移的规律“上加下减,左加右减”,按照题意改写解析式即可. 抛物线y=(x+1)2向下平移2个单位,得 y=(x+1)2-2, 再向右平移1个单位,得 y=[(x-1)+1]2-2=x2-2, 即y=x2-2. 故本题应选D.查看答案和解析>>
科目: 来源:贵州省遵义市2018届九年级(上)第一次月考数学试卷 题型:单选题
在一定的条件下,若物体运动的路程s(米)与时间t(秒)的关系式为s=5t2+2t,则当t=4秒时,该物体所经过的路程为( )
A. 28米 B. 48米 C. 68米 D. 88米
D 【解析】当t=4时,s=5t2+2t=5×42+2×4=80+8=88m,故选D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com