
科目: 来源:2017学年嘉定区第一学期九年级期终学业质量调研测试(2018年初三一模) 题型:填空题
如果一个斜坡的坡度i=1: 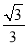 ,那么该斜坡的坡角为_____度.
,那么该斜坡的坡角为_____度.
查看答案和解析>>
科目: 来源:2017学年嘉定区第一学期九年级期终学业质量调研测试(2018年初三一模) 题型:填空题
已知弓形的高是1厘米,弓形的半径长是13厘米,那么弓形的弦长是_____厘米.
10 【解析】试题解析:如图, 过圆心O作OD⊥AB,交弧于C.则CD=1,连接OA. 在直角△AOD中,OA=13,OD=13-CD=12, 则AD==5, ∴AB=2AD=10. 故答案是:10.查看答案和解析>>
科目: 来源:2017学年嘉定区第一学期九年级期终学业质量调研测试(2018年初三一模) 题型:填空题
已知⊙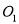 的半径长为4,⊙
的半径长为4,⊙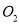 的半径长为
的半径长为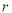 ,圆心距
,圆心距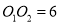 ,当⊙
,当⊙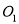 与⊙
与⊙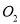 外切时,
外切时, 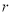 的长为____.
的长为____.
查看答案和解析>>
科目: 来源:2017学年嘉定区第一学期九年级期终学业质量调研测试(2018年初三一模) 题型:填空题
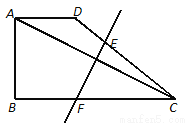
如图,在直角梯形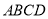 中,
中, 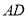 ∥
∥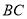 ,
, 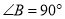 ,
, 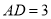 ,
, 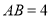 ,
, 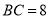 ,点
,点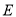 、
、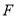 分别在边
分别在边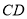 、
、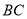 上,联结
上,联结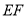 .如果△
.如果△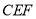 沿直线
沿直线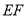 翻折,点
翻折,点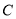 与点
与点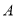 恰好重合,那么
恰好重合,那么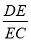 的值是____.
的值是____.
查看答案和解析>>
科目: 来源:2017学年嘉定区第一学期九年级期终学业质量调研测试(2018年初三一模) 题型:解答题
已知二次函数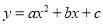 的图像上部分点的坐标
的图像上部分点的坐标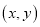 满足下表:
满足下表:
| … |
|
|
|
| … |
| … |
|
|
|
| … |
(1)求这个二次函数的解析式;
(2)用配方法求出这个二次函数图像的顶点坐标和对称轴.
(1)(2)顶点坐标为; 对称轴是直线 【解析】试题分析:(1)运用待定系数法求解即可; (2)运用配方法得y,从而求出顶点坐标和对称轴. 试题解析:(1)由题意,得 解这个方程组,得 , 所以,这个二次函数的解析式是. (2) 顶点坐标为; 对称轴是直线.查看答案和解析>>
科目: 来源:2017学年嘉定区第一学期九年级期终学业质量调研测试(2018年初三一模) 题型:解答题
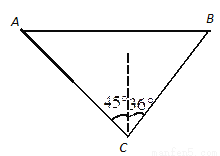
如图,某湖心岛上有一亭子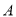 ,在亭子
,在亭子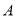 的正东方向上的湖边有一棵树
的正东方向上的湖边有一棵树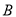 ,在这个湖心岛的湖边
,在这个湖心岛的湖边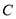 处测得亭子
处测得亭子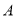 在北偏西
在北偏西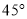 方向上,测得树
方向上,测得树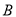 在北偏东
在北偏东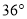 方向上,又测得
方向上,又测得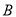 、
、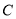 之间的距离等于
之间的距离等于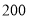 米,求
米,求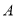 、
、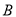 之间的距离(结果精确到
之间的距离(结果精确到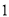 米).
米).
(参考数据: 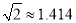 ,
, 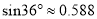 ,
, 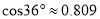 ,
, 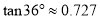 ,
, 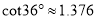 )
)
查看答案和解析>>
科目: 来源:2017学年嘉定区第一学期九年级期终学业质量调研测试(2018年初三一模) 题型:解答题
如图,在Rt△ABC中,∠C=90°,AC=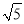 ,BC=2
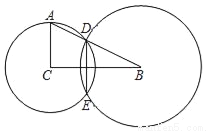
,BC=2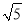 ,以点C为圆心,CA长为半径的⊙C与边AB交于点D,以点B为圆心,BD长为半径的⊙B与⊙C另一个交点为点E.
,以点C为圆心,CA长为半径的⊙C与边AB交于点D,以点B为圆心,BD长为半径的⊙B与⊙C另一个交点为点E.
(1)求AD的长;
(2)求DE的长.
查看答案和解析>>
科目: 来源:2017学年嘉定区第一学期九年级期终学业质量调研测试(2018年初三一模) 题型:解答题
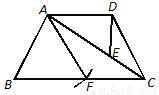
如图,已知梯形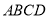 中,
中, 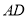 ∥
∥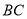 ,
, 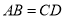 ,点
,点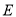 在对角线
在对角线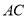 上,且满足
上,且满足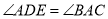 .
.
(1)求证: 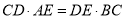 ;
;
(2)以点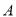 为圆心,
为圆心, 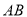 长为半径画弧交边
长为半径画弧交边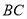 于点
于点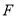 ,联结
,联结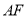 .
.
求证: 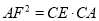 .
.
查看答案和解析>>
科目: 来源:2017学年嘉定区第一学期九年级期终学业质量调研测试(2018年初三一模) 题型:解答题
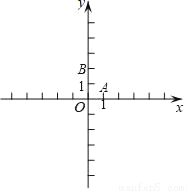
已知在平面直角坐标系xOy(如图)中,已知抛物线y=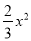 +bx+c点经过A(1,0)、B(0,2).
+bx+c点经过A(1,0)、B(0,2).
(1)求该抛物线的表达式;
(2)设该抛物线的对称轴与x轴的交点为C,第四象限内的点D在该抛物线的对称轴上,如果以点A、C、D所组成的三角形与△AOB相似,求点D的坐标;
(3)设点E在该抛物线的对称轴上,它的纵坐标是1,联结AE、BE,求sin∠ABE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com