
科目: 来源:安徽省六安市2018届九年级上学期第二次月考数学试卷 题型:单选题
以正方形ABCD的BC边为直径作半圆O,过点D作直线切半圆于点F,交AB边于点E.则三角形ADE和直角梯形EBCD周长之比为( )
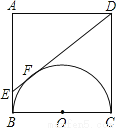
A. 4:5 B. 5:6 C. 6:7 D. 7:8
C查看答案和解析>>
科目: 来源:安徽省六安市2018届九年级上学期第二次月考数学试卷 题型:填空题
已知⊙O的直径为10 cm,圆心O到直线l的距离是 7 cm.,那么直线l和⊙O的位置关系是: ________.
相离 【解析】根据题意求出⊙O的半径为5,由和圆心O到直线l的距离是7cm,可知r<d,比较即可知直线l和⊙O的位置关系是相离. 故答案为:相离.查看答案和解析>>
科目: 来源:安徽省六安市2018届九年级上学期第二次月考数学试卷 题型:填空题
一点和⊙O上的最近点距离为4cm,最远距离为9cm,则这个圆的半径是______.
6.5cm或2.5cm 【解析】试题解析:点P应分为位于圆的内部与外部两种情况讨论: ①当点P在圆内时,最近点的距离为4cm,最远点的距离为9cm,则直径是4+9=13cm,因而半径是6.5cm; ②当点P在圆外时,最近点的距离为4cm,最远点的距离为9cm,则直径是9?4=5cm,因而半径是2.5cm. 故答案为6.5cm或2.5cm.查看答案和解析>>
科目: 来源:安徽省六安市2018届九年级上学期第二次月考数学试卷 题型:填空题
如图,在半径为3的⊙O中,直径AB与弦CD相交于点E,连接AC,BD.若AC=2,则cosD=________.
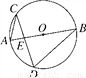
查看答案和解析>>
科目: 来源:安徽省六安市2018届九年级上学期第二次月考数学试卷 题型:填空题
如图,在平面直角坐标系中,已知点A(2,0),B(2-a,0),C(2+a,0) (a>0),点P在以D(5,4)为圆心,半径为1的圆上运动,且始终满足∠BPC=90°,则a的最大值是________
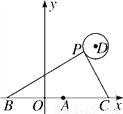
查看答案和解析>>
科目: 来源:安徽省六安市2018届九年级上学期第二次月考数学试卷 题型:解答题
如图,图形中每一小格正方形的边长为1,已知△ABC
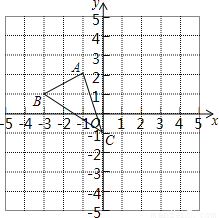
(1)AC的长等于 .(结果保留根号)
(2)将△ABC向右平移2个单位得到△A′B′C′,则A点的对应点A′的坐标是 ;
(3)画出将△ABC绕点C按顺时针方向旋转90°后得到△A1B1C1,并写出A点对应点A1的坐标?
(1)(2)(1,2)(3)图形见解析 【解析】试题分析:(1)根据图形,可得出AC的坐标,可得纵横坐标的关系,进而可求出AC的长; (2)根据图形,可得出ABC的坐标,向右平移2个单位可得A'的坐标; (3)根据旋转的规律,把△OAB的绕点O按顺时针方向旋转90°,就是把它上面的各个点按顺时针方向旋转90°,可得A1的坐标. 试题解析:(1)根据勾股定理可得AC=; (2)...查看答案和解析>>
科目: 来源:安徽省六安市2018届九年级上学期第二次月考数学试卷 题型:解答题
数学拓展课程《玩转学具》课堂中,小陆同学发现:一副三角板中,含45°的三角板的斜边与含30°的三角板的长直角边相等,于是,小陆同学提出一个问题:如图,将一副三角板直角顶点重合拼放在一起,点B,C,E在同一直线上,若BC=2,
求AF的长.(结果保留根号)
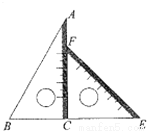
查看答案和解析>>
科目: 来源:安徽省六安市2018届九年级上学期第二次月考数学试卷 题型:解答题
如图,已知正六边形ABCDEF,其外接圆的半径是a,求正六边形的周长和面积.
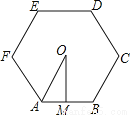
求⊙O的半径.
【解析】试题分析:根据正六边形的半径等于边长进行解答即可. 试题解析:∵正六边形的半径等于边长, ∴正六边形的边长AB=OA=a; 正六边形的周长=6AB=6a;. 在Rt△OAM中 ∵OM=OA•sin60°=a, 正六边形的面积S=6××a×a=a2.查看答案和解析>>
科目: 来源:安徽省六安市2018届九年级上学期第二次月考数学试卷 题型:解答题
如图,已知AB是⊙O的弦,P是AB上一点,AB=10,PA=4,OP=5,求⊙O的半径.
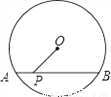
查看答案和解析>>
科目: 来源:安徽省六安市2018届九年级上学期第二次月考数学试卷 题型:解答题
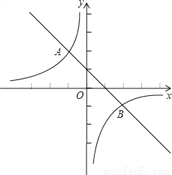
如图,已知一次函数y=kx+b与反比例函数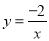 的图象交于A(﹣1,m)、B(n,﹣1)两点.
的图象交于A(﹣1,m)、B(n,﹣1)两点.
(1)求出A、B两点的坐标;
(2)求出这个一次函数的表达式;
(3)根据图象,写出使一次函数值大于反比例函数值的x的范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com