
科目: 来源:云南省2017-2018学年八年级上学期期末考试数学试卷 题型:填空题
一艘轮船在静水中的速度为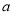 千米/时,水流速度为
千米/时,水流速度为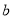 千米/时,若A、B两个港口之间的距离为50千米,则该轮船在A、B间往返一次所需时间为_________小时.
千米/时,若A、B两个港口之间的距离为50千米,则该轮船在A、B间往返一次所需时间为_________小时.
查看答案和解析>>
科目: 来源:云南省2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
计算:(-1)2017 +(π-3.14)0-(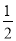 )3
)3
查看答案和解析>>
科目: 来源:云南省2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
化简:x(x2+x-1)-(2x2-1)(x-4)
原式= 【解析】试题分析: 根据多项式的乘法法则去掉括号,再合并同类项即可. 试题解析: 原式=( )- () = – = .查看答案和解析>>
科目: 来源:云南省2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
解方程: 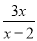 +
+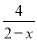 =1
=1
查看答案和解析>>
科目: 来源:云南省2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
如图,AB=AD,BC=DC,求证:∠ABC=∠ADC.
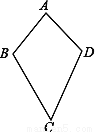
查看答案和解析>>
科目: 来源:云南省2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
先化简,再求值: 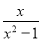 ÷(1+
÷(1+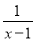 ),其中
),其中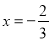 .
.
查看答案和解析>>
科目: 来源:云南省2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
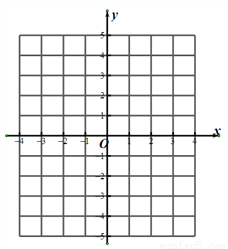
平面直角坐标系中,△ABC的三个顶点坐标分别为A(0,4),B(2,4),C(3,-1).
(1)试在平面直角坐标系中,标出A、B、C三点;
(2)求△ABC的面积.
(3)若△A1B1C1与△ABC关于x轴对称,写出A1、B1、C1的坐标,并画出△A1B1C1。
查看答案和解析>>
科目: 来源:云南省2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
马小虎的家距离学校2000米,一天马小虎从家去上学,出发10分钟后,爸爸发现他的教学课本忘记拿了,立即带上课本去追他,在距离学校400米的地方追上了他,已知爸爸的速度是马小虎速度的2倍,求马小虎的速度.
马小虎的速度为80米/分. 【解析】试题分析:设马小虎的速度为x米/分,则爸爸的速度为2x米/分,根据题意可得,小马虎和爸爸同时走1600米,爸爸少用10分钟,据此列方程求解. 试题解析:【解析】 设马小虎的速度为x米/分,则爸爸的速度为2x米/分, 由题意得: 解得:x=80,经检验,x=80是原分式方程的解,且符合题意. 答:马小虎的速度为80米/分.查看答案和解析>>
科目: 来源:云南省2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
如图,在△ABC中,∠C=∠ABC=2∠A,BD是AC边上的高,求∠DBC的度数.
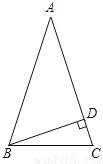
查看答案和解析>>
科目: 来源:云南省2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
在△ABC中,BC=AC,∠BCA=90°,P为直线AC上一点,过点A作AD⊥BP于点D,交直线BC于点Q.
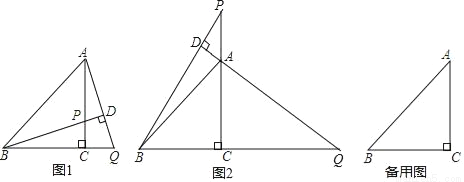
(1)如图1,当P在线段AC上时,求证:BP=AQ;
(2)如图2,当P在线段CA的延长线上时,(1)中的结论是否成立? (填“成立”或“不成立”)
(3)在(2)的条件下,当∠DBA= 度时,存在AQ=2BD,说明理由.
(1)证明见解析;(2)(2)成立,理由见解析;(3)当∠DBA=22.5°时,存在AQ=2BD,理由见解析. 【解析】试题分析:(1)首先根据内角和定理得出∠DAP=∠CBP,进而得出 △ACQ≌△BCP即可得出答案; (2)延长BA交PQ于H,由于 得到 推出△AQC≌△BPC(ASA),即可得出结论; (3)当时,存在根据等腰三角形的性质得到BP=2BD,通过△PBC≌△AC...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com