
科目: 来源:江苏省南京市建邺区2016-2017学年度第一学期期末调研测试九年级数学试卷 题型:填空题
如图,AB=5,P是线段AB上的动点,分别以AP、BP为边,在线段AB的同侧作正方形APCD和正方形BPEF,连接CF,则CF的最小值是____.
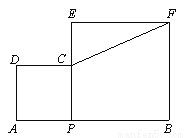
查看答案和解析>>
科目: 来源:江苏省南京市建邺区2016-2017学年度第一学期期末调研测试九年级数学试卷 题型:解答题
(1)解方程:x2-4x+2=0; (2)计算:sin30°-cos245°+tan60°·sin60°.
(1), ;(2). 【解析】试题分析:(1)利用配方法,再直接开平方法解方程,(2)根据特殊三角函数值求解即可. 试题解析:(1)x2-4x=-2, (x-2)2=2, x-2=±, x1=2+,x2=2-. (2) sin30°-cos245°+tan60°·sin60° 原式=, =, =.查看答案和解析>>
科目: 来源:江苏省南京市建邺区2016-2017学年度第一学期期末调研测试九年级数学试卷 题型:解答题
已知关于x的方程(k-2)x2-(k-2)x+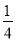 =0有两个相等的实数根.求k的值.
=0有两个相等的实数根.求k的值.
查看答案和解析>>
科目: 来源:江苏省南京市建邺区2016-2017学年度第一学期期末调研测试九年级数学试卷 题型:解答题
某校九年级有24个班,共1 000名学生,他们参加了一次数学测试.学校统计了所有学生的成绩,得到下列统计图.
(1)求该校九年级学生本次数学测试成绩的平均数;
(2)下列关于本次数学测试说法正确的是( )
A.九年级学生成绩的众数与平均数相等
B.九年级学生成绩的中位数与平均数相等
C.随机抽取一个班,该班学生成绩的平均数等于九年级学生成绩的平均数
D.随机抽取300名学生,可以用他们成绩的平均数估计九年级学生成绩的平均数
(1)81分;(2)D. 【解析】试题分析:根据加权平均数的计算方法即可求解,(2)九年级学生成绩的众数是80,平均分是81,因此A错误,九年级学生成绩的中位数是80,平均分是81,因此B错误,因为每个班的平均成绩不一定相等,因此C错误,故选D. 试题解析:(1)80×60%+82.5×40%=81(分), (2)D.查看答案和解析>>
科目: 来源:江苏省南京市建邺区2016-2017学年度第一学期期末调研测试九年级数学试卷 题型:解答题
从甲、乙、丙、丁4名同学中随机抽取环保志愿者.求下列事件的概率:
(1)抽取1名,恰好是甲;
(2)抽取2名,甲在其中.
(1) ;(2) . 【解析】试题分析:(1)根据概率的求法,找准两点:①全部等可能情况的总数;②符合条件的情况数目;二者的比值就是其发生的概率.因此,由从甲、乙、丙3名同学中随机抽取环保志愿者,直接利用概率公式求解即可求得答案. (2)利用列举法可得抽取2名,可得:甲乙,甲丙,乙丙,共3种等可能的结果,甲在其中的有2种情况,然后利用概率公式求解即可求得答案. 试题解析:(1)∵...查看答案和解析>>
科目: 来源:江苏省南京市建邺区2016-2017学年度第一学期期末调研测试九年级数学试卷 题型:解答题
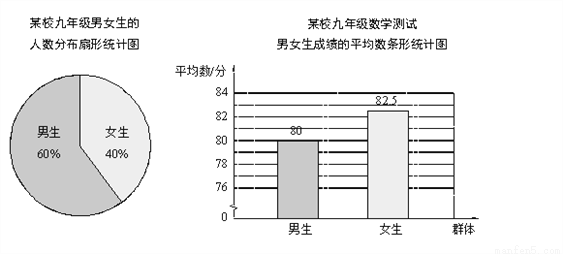
如图,点C在⊙O上,弦AB⊥OC,垂足为D,AB=8,CD=2.求⊙O的半径.
查看答案和解析>>
科目: 来源:江苏省南京市建邺区2016-2017学年度第一学期期末调研测试九年级数学试卷 题型:解答题
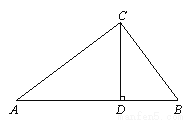
如图,在△ABC中,CD是边AB上的高,且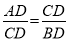 ,求∠ACB的大小.
,求∠ACB的大小.
查看答案和解析>>
科目: 来源:江苏省南京市建邺区2016-2017学年度第一学期期末调研测试九年级数学试卷 题型:解答题
已知二次函数y=-x2+bx+c的图像经过点(0,3)、(-1,0).
(1)求二次函数的表达式;
(2)在给定的平面直角坐标系中,画出这个二次函数的图像;
(3)根据图像,直接写出当x满足什么条件时,y>0.
查看答案和解析>>
科目: 来源:江苏省南京市建邺区2016-2017学年度第一学期期末调研测试九年级数学试卷 题型:解答题
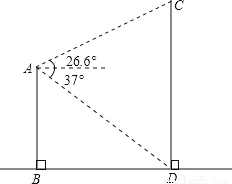
如图,平地上一幢建筑物AB与铁塔CD相距40m,在建筑物的顶部测得铁塔底部的俯角为37°,测得铁塔顶部的仰角为26.6°,求铁塔的高度.
(参考数据:sin26.6°≈0.45,tan26.6°≈0.50;sin37°≈0.60,tan37°≈0.75)
查看答案和解析>>
科目: 来源:江苏省南京市建邺区2016-2017学年度第一学期期末调研测试九年级数学试卷 题型:解答题
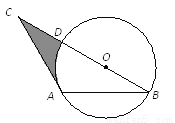
如图,在△ABC中,AB=AC,∠B=30°,O是BC上一点,以点O为圆心,OB长为半径作圆,恰好经过点A,并与BC交于点D.
(1)求证:CA是⊙O的切线.
(2)若AB=2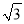 ,求图中阴影部分的面积(结果保留π).
,求图中阴影部分的面积(结果保留π).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com