
科目: 来源:海南省定安县2018届九年级上学期期末考试数学试卷 题型:单选题
将一元二次方程x2-4x-6=0化成(x-a)2=b的形式,则b等于( )
A. 4 B. 6 C. 8 D. 10
D 【解析】利用配方法即可得出答案. 【解析】 ∵, , , , ∴b=10. 故选D.查看答案和解析>>
科目: 来源:海南省定安县2018届九年级上学期期末考试数学试卷 题型:单选题
如图,铁路路基横断面为一个等腰梯形,若腰的坡度为i=3:2,顶宽是7米,路基高是6米,则路基的下底宽是( )
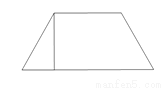
A. 7米 B. 11米 C. 15米 D. 17米
C 【解析】可过上底的两个端点,分别作下底的垂线段,根据腰的坡度和梯形的高求出下底的长. 【解析】 如图所示 ,等腰梯形ABCD是铁路路基的横断面,腰AB、CD的坡度为3: 2,BC=7米,BE=CF=6米. 在Rt△ABE中, tanA=,BE=6米, ∴AE==4米, ∴DF=AE=4米, ∴AD=AE+EF+FD=AE+BC+FD=4+7+4=15...查看答案和解析>>
科目: 来源:海南省定安县2018届九年级上学期期末考试数学试卷 题型:单选题
如图,为测量一棵与地面垂直的树OA的高度,在距离树的底端25米的B处,测得树顶A的仰角∠ABO为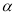 ,则树OA的高度为 ( )
,则树OA的高度为 ( )
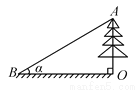
A. 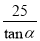 米 B. 25
米 B. 25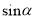 米 C. 25
米 C. 25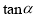 米 D. 25
米 D. 25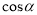 米
米
查看答案和解析>>
科目: 来源:海南省定安县2018届九年级上学期期末考试数学试卷 题型:单选题
参加一次足球联赛的每两队之间都进行一场比赛,共有比赛55场,总共有( )支球队参加比赛.
A. 9 B. 10 C. 11 D. 12
C 【解析】每个队都要与其余队比赛一场,而两队之间只赛1场.所以等量关系为:队的个数×(队的个数-1)×=55,把相关数值代入计算即可. 【解析】 设有x队参加比赛. x(x?1)=55, (x?11)(x+10)=0, 解得x1=11,x2=?10(不合题意,舍去). 故选C.查看答案和解析>>
科目: 来源:海南省定安县2018届九年级上学期期末考试数学试卷 题型:单选题
某班为迎接“体育健康周”活动,从3 名学生(1男 2女)中随机选两名担任入场式旗手,则选中两名女学生的概率是( )
A. 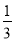 B.
B. 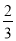 C.
C. 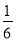 D.
D. 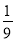
查看答案和解析>>
科目: 来源:海南省定安县2018届九年级上学期期末考试数学试卷 题型:单选题
如图,在Rt△ABC中,∠C=90°,∠CAB的平分线交BC于D,DE是AB的垂直平分线,垂足为E.若BC=6,则DE的长为( )
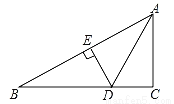
A. 1 B. 2 C. 3 D. 4
B 【解析】首先根据角平分线的性质得到DE=DC,∠BAD=∠CAD,由垂直平分线的性质可得AD=BD,结合等边对等角和等量代换的知识可得∠B=∠BAD=∠CAD;然后根据∠C=90°,即可求得∠B=30°,在Rt△BDE中,然后根据含有30°角的直角三角形的性质,得出BD=2DE,即可解答. 【解析】 ∵AD平分∠BAC,∠C=90°,DE⊥AB, ∴DE=DC,∠B+∠BA...查看答案和解析>>
科目: 来源:海南省定安县2018届九年级上学期期末考试数学试卷 题型:单选题
如图,在平面直角坐标系中,△ABC位于第二象限,点C的坐标是(﹣1,1),先把△ABC向右平移5个单位长度得到△A1B1C1,再作与△A1B1C1关于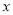 轴对称的△A2B2C2,则点C的对应点C2的坐标是( )
轴对称的△A2B2C2,则点C的对应点C2的坐标是( )
A. (4,1) B. (4,-1) C. (﹣6,1) D. (-6,-1)
B 【解析】首先利用平移的性质得到△A1B1C1,进而利用关于x轴对称点的性质得到△A2B2C2,即可得出答案. 【解析】 如图所示:点C的对应点C2的坐标是:(4,?1). 故选:B.查看答案和解析>>
科目: 来源:海南省定安县2018届九年级上学期期末考试数学试卷 题型:填空题
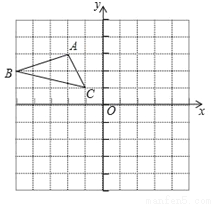
计算: 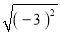 =_______.
=_______.
查看答案和解析>>
科目: 来源:海南省定安县2018届九年级上学期期末考试数学试卷 题型:填空题
在△ABC中,∠C=90°,AB=10,BC=8,则cos A=________.
【解析】先利用勾股定理求出AC的长,再利用锐角三角函数关系得出cosA=,即可得出答案. 【解析】 如图所示, ∵∠C=90°,AB=10,BC=8, 由勾股定理得,AC=, ∴cosA= ==. 故答案为: .查看答案和解析>>
科目: 来源:海南省定安县2018届九年级上学期期末考试数学试卷 题型:填空题
如图,在Rt△ABC中,∠BAC=90°,AB=4,AC=3,AD⊥BC于点D,则△ACD与△ABC的面积比为_________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com